Variational AutoEncoder(VAE) 이해

Copyright of Image : Joseph Rocca

from Medium “Understanding Variational Autoencoder” https://towardsdatascience.com/understanding-variational-autoencoders-vaes-f70510919f73

• endcoding distribution이 학습 중에 regularised 되는 오토인코더
• regularised 됨에 따라 latent space 가 몇몇 새로운 데이터를 generate 하도록 도움.
• 즉 Autoencoder + (Reglularisation + Variational inference) 결합

오토인코더

• 차원축소(encoding) 후 복귀(decoding)과정을 통해 원래의 신호를 복원
• 재구성오차(Reconstruction error)가 손실 함수가 됨
• 차원이 축소되어 정보의 일부가 손실됨. 즉 목표는 꼭 필요한 특징만 추출하는 것
• 단일 선형, 수직(orthonomal) 행렬로 차원을 축소하는 PCA와는 달리 비선형 layer을 여러개 연결한 모델을 통해 차원을 축소함.
• 선형 오토인코더는 PCA와 basis가 수직이 아니라는 점이 다름
• 오토 인코더의 특징 두가지를 명심!!
  • Lack of regularity : 재구성 오차가 거의 없는 차원 축소는 대가가 있음. Latent space에서 이해할만한, 추출할 구조가 없다.
  • 위 차원축소는 데이터의 차원을 줄이면서 대부분의 데이터 구조 정보를 감소된 차원에 저장한다는 것

VAE

• Content generation의 관점
  • Q : latent space가 잘 구축이 되었다면(Well organized, regular enough) 아무 지점에서의 latent space의 점을 잡아 decode 해서 새로운 데이터를 만들 수 있지 않을까?
  • A: No!!!!! latent space의 regularity는 Initial space의 데이터의 분포, latent space의 차원, 인코더의 구조에 영향을 받는 어려운 부분이다.
    • ex) 오토인코더의 자유도가 높을 수록 정보의 손실 없이 데이터를 encode, decode할 수 있지만 이는 과적합을 불러옴. 즉 몇몇 latent space의 값들이 의미없는 content를 뱉는다는 것.
  • 즉 오토인코더가 latent space가 어찌되던 간에 해당 데이터의 재구성에만 신경 쓰는 것이 문제(과적합 문제)
• VAE는 이러한 과적합을 해결하고 latent space에서 generative process를 가능하게 해 주는 알고리즘.
• Latent space의 regularisation을 돕기 위해 encoding/decoding를 약간 바꿈 : Input을 점으로 인코딩 하는 것이 아니라 latent space의 확률로 인코딩해버림
• 학습 과정
  1. Input이 latent space의 분포로 인코딩됨
  2. 샘플링에 의해 latent space의 점들이 뽑힘
  3. 이렇게 뽑힌 점들이 decode되고 재구성오차가 계산됨
  4. 재구성 오차가 네트워크 상에서 backpropagated됨
• 일반적으로는 encoded한 확률이 정규분포로 정해져 평균과 분산 행렬을 뱉도록 학습된다.
• 입력 데이터가 점이 아니라 확률로 인코딩 되는 점이 regularisation 부분임
• 즉 Loss function은 마지막 층에서 “reconstruction 항”, latent 층에서 “regularisation 항”을 포함하게 된다.
• Regularisation 항은 획득된 확률과, 일반 가우시안 분포의 KLD로 표현된다.

Regularisation 란?

• 다음의 두 속성 만족
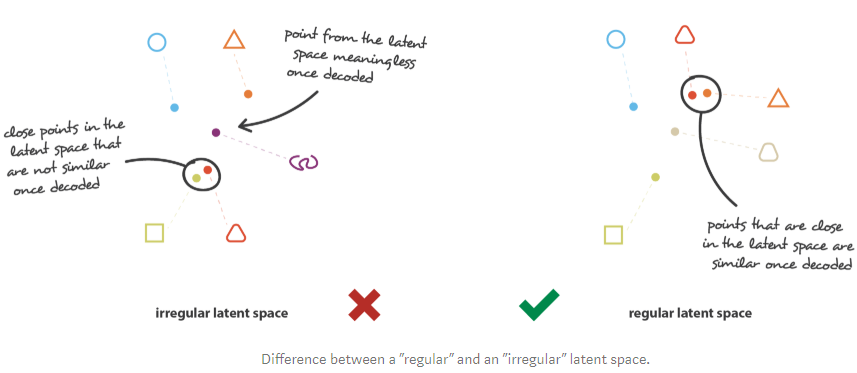
  • Continuity : latent space의 두 점이 디코딩 했을 때 완전 다른 값을 주지 않음
  • Completeness : 정해진 분포 안에서의 샘플된 점을 디코딩 했을 때 “의미있는” 값을 나타내야 함
• Regularisation항을 추가하지 않으면 VAE는 기존오토인코더와 비슷하게 작은 분산 또는 서로 멀리 떨어져 있는 다른 평균값들을 반환한다.
• 즉 우리는 encoding된 Covariance matrix와 mean을 regularise해아함
• Regluarise는 reconsctruction error를 대가로 이루어짐. 즉 이 문제는 Tradeoff between Reconstruction error and KLD
• Regularise 된 데이터는 “gradient“를 만드는 경향이 있다.