cs230_lec6_C4W1

(From : deeplearningai https://www.youtube.com/watch?time_continue=386&v=AwQHqWyHRpU)

Computer vision

• 딥러닝의 발전과 같이 발전중인 분야
• 이미지 분류, 물체 인식, 사진 스타일 전환(Neural Style Transfer) 등등
• 컴퓨터 비전에서의 딥러닝의 발전이 기대가 되는 이유
  • 빠른 발전이 많은 새로운 어플리케이션을 만들어지게 함
  • 컴퓨터 비전 시스템을 구축하지 않아도 서로 신경망 구조와 알고리즘에 많은 영감을 줌.
    • ex) 음성인식 시 컴퓨터 비전의 개념 사용
• 이미지 인식에서의 딥러닝
  • 이미지 해상도에 따라서 node의 수가 기하급수적으로 많아질 수 있음
  • 이를 해결한 것이 합성곱 연산

Edge Detection

• 일반적인 이미지 인식 과정- 갈수록 더 복잡한 특징을 인지
• 합성곱 신경망을 거친 후 이미지의 수직, 수평 모서리가 인식됨
• 이번강의에서는 신경망의 하위층이 모서리와 선을 어떻게 인식하는지에 대해서 배움
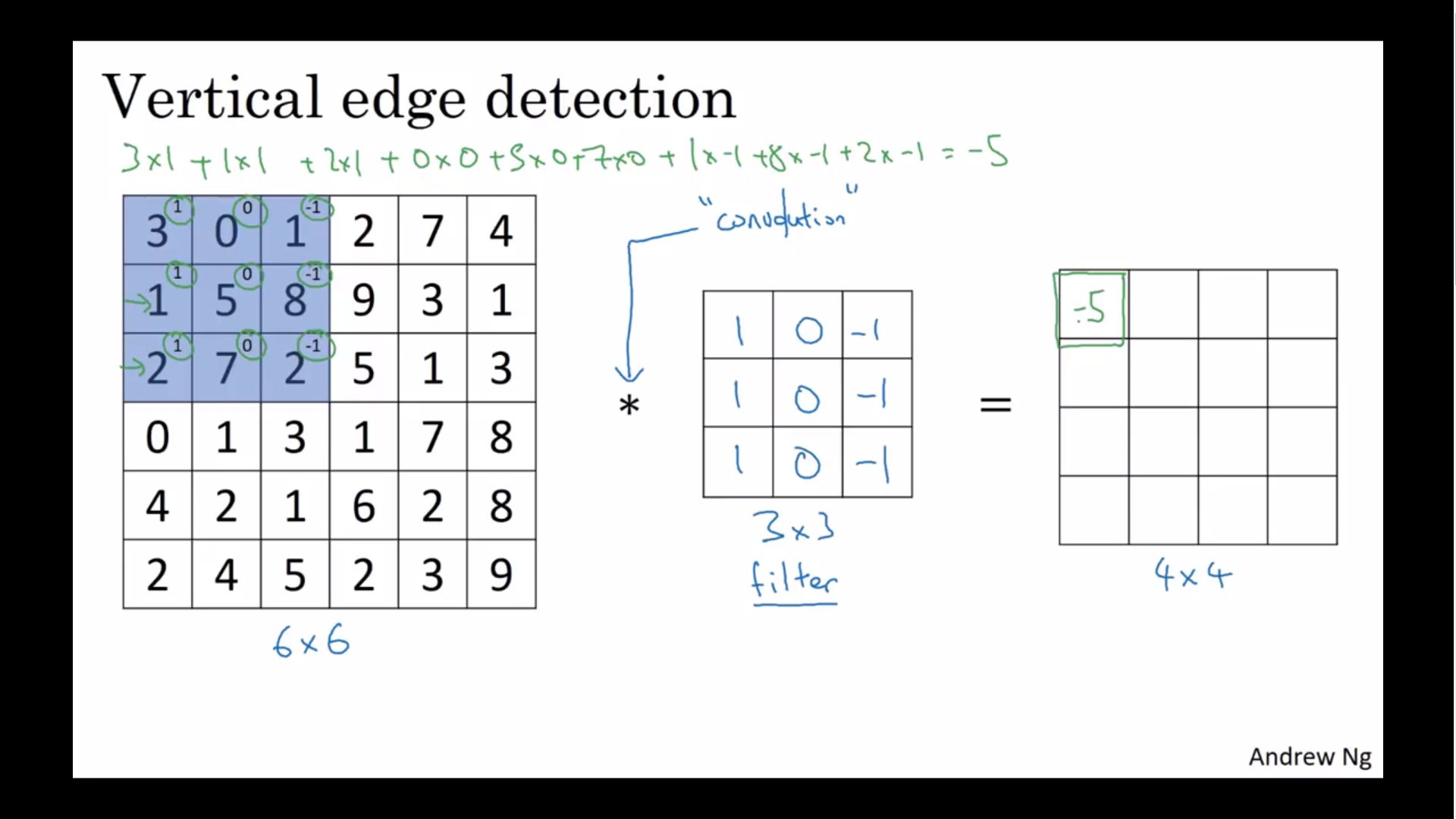
• 이미지에 정사각형의 필터(커널)을 합성곱해줌
  • ${*}$ 의 의미 : 수학에서는 곱셈, 파이썬 에서는 성분곱
  • python : Conv-forward
  • tensorflow : tf.nn.conv2d
  • Keras : Conv2D
• 이것이 바로 수직 모서리를 인식하는 원리
• 보다 자세한 설명은 아래 그림을 보면 알 수 있다.
• 모서리의 스케일의 차이가 있지만, 실제로 엄청 큰 이미지에 대해서 진행하면 꽤나 정교한 수직 경계선을 찾을 수 있다.
• Sobel Filter, Scharr Filter (중간부분에 더 초점을 둠)
• 딥러닝을 하면 파라미터는 자동으로 학습됨

Padding

• 합성곱 계산시 행렬이 줄어드는 것을 방지하고자 하는 것
• 이미지 가장자리의 정보를 고려하고자 하는 것
• 가장자리에 0으로 된 층을 덧대는 것
• Valid Convolution : padding 없는 것
• Same Convolution : 입력 이미지와 같게 padding하는 것
  • $p=\frac{f-1}{2}$
• 컴퓨터 비전에는 필터가 보통 홀수, padding을 비대칭으로 만들지 않기 위해서임

Strided convolution

• 합성곱을 얼마나 이동하면서 계산할 지 정하는 것
• n X n image, f X f filter, padding p, stride s 일때
  • $[\frac{n+2p-f}{s}+1]$ X $[ \frac{n+2p-f}{s}+1]$
• 미러링(Mirroring) : 필터를 가로 세로로 뒤집은 뒤에 계산함
  • 일반적으로 딥러닝은 이를 생략함
  • 수학자들은 합성곱을 교차상관으로 부름

3차원 Convolution

• 일반적으로 이미지는 RGB로 채널이 3개임
• 이미지와 필터의 채널의 수가 같아야 함

합성곱 층의 레이어 분석

• 3X3X3 필터 파라미터 수 : 27+1(bias)
• 이미지가 아무리 크던 작던 파라미터 수는 고정되어 있다(각 필터 파라미터 수 * 필터 개수)

풀링(Pooling)

• 하이퍼파라미터(filter size, stride, Max or average pooling)
  • Max pooling : 거의 대부분 사용
  • Average pooling : 거의 안씀
• 학습할 파라미터가 없음

합성곱의 장점

• 파라미터 수가 더 적게 필요하다
  • FC 파라미터 수 :$n_{input} \times n_{output}$
  • Conv 파라미터 수 : $n_{filter} \times n_{filter} \times n_{filter}$
  • 변수를 공유하기 때문임 (Parameter sharing)
  • 연결된 픽셀 값만 영향을 줌 (Sparcity of connection)