cs230_lec4_C2W3

Updated: November 20, 2019

(From : deeplearningai https://www.youtube.com/watch?time_continue=386&v=AwQHqWyHRpU)

하이퍼파라미터 튜닝 작업

중요한 순서
1. $\alpha$
2. minibatch size, momentum(\beta), # of hidden units
3. # of layers, learning rate decay
4. $\beta_1, \beta_2, \epsilon (ADAM)
임의의 값 대입해보기
- 머신러닝 방식(하이퍼파라미터가 적을 때) :Grid로 구하기
- 딥러닝 방식 : 아무렇게나 점 찍고 구해보기
  - 어떤 하이퍼파라미터가 문제에서 중요한지 모르기 때문
- 임의의 값 대입할 때 중요한 점
  - 스케일 맞추기 linear scale vs log scale
  - sensitivity 때문임
Coarse to fine(정밀화 법칙)
- 대충 최적화 점을 찾은 뒤에 그 부근을 확대하여 추가로 진행

머신 러닝처럼 각 node의 값들을 정규화 하는 것을 의미
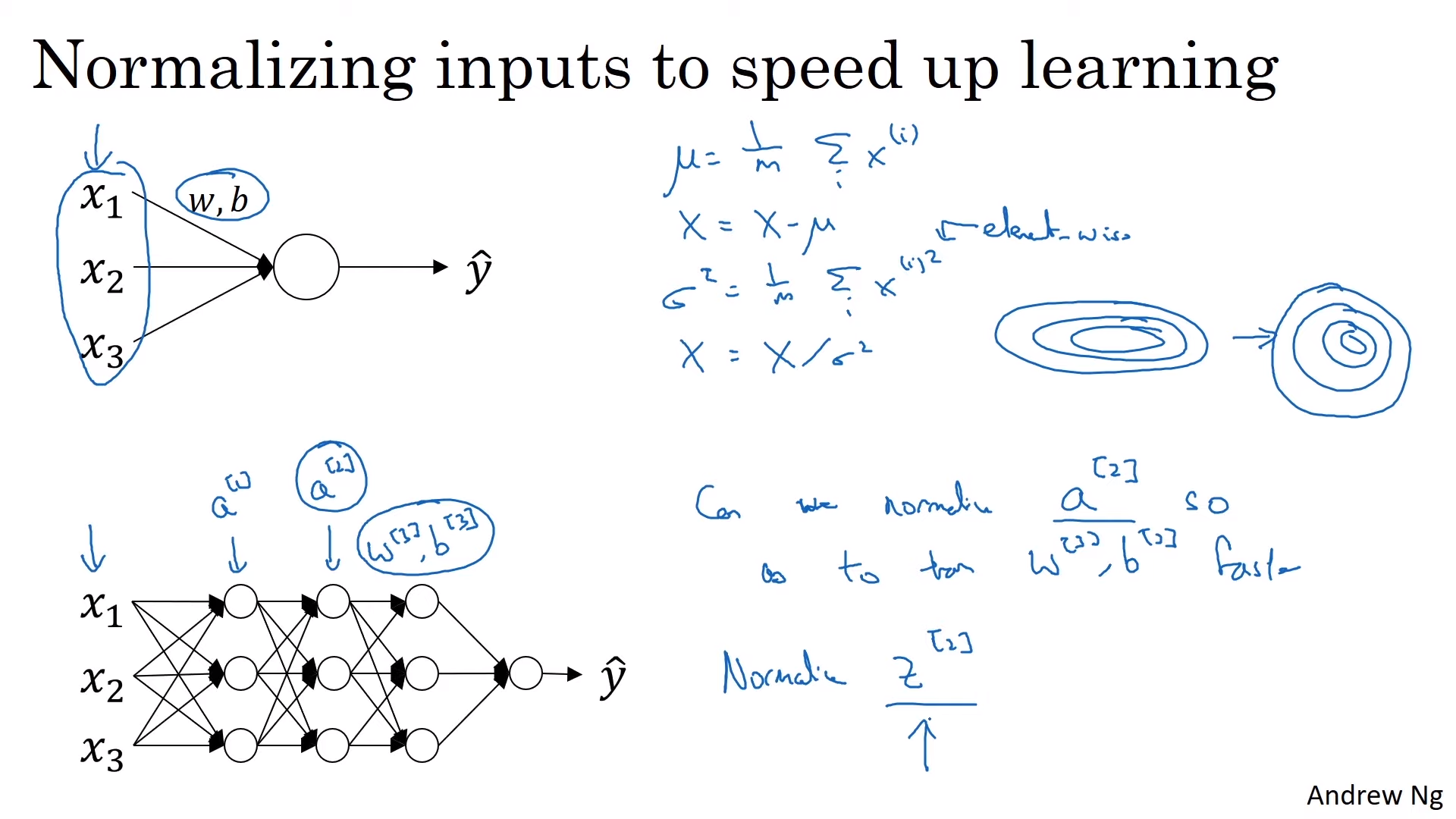
- W와 b 값을 잘 정하기 위해서 Z값을 많이 정규화함
- z값을 평균 0, 분산 1로 정규화 하는 것은 항상 좋지는 않음. 다양한 분포를 가져야 하기 때문
- 따라서 $\hat{z}$를 계산함
- 학습 알고리즘에서 선택할 수 있는 $\gamma, \beta$ 값을 통해 은닉 유닛이 서로 다른 분산, 평균 값을 같게 할 수 있음
Activation 이전에 이루어짐
미니배치에 대해서도 각 미니배치값을 이용해서 평균, 분산을 따로 계산해서 진행
어떤 상수를 정해줘도 $b$는 평균을 빼주기 때문에 필요없는 변수임.
즉 $z^{[l]}=W^{[l]}a^{[l-1]}$
b대신 bias를 처리하는 것은 $\beta$ 항이 됨

Covariance shift
- X,Y에 대해서 학습시킬 때 X의 분포가 바뀐다면 학습을 다시 해야 함
- 관측함수가 바뀌지 않아도 그러함
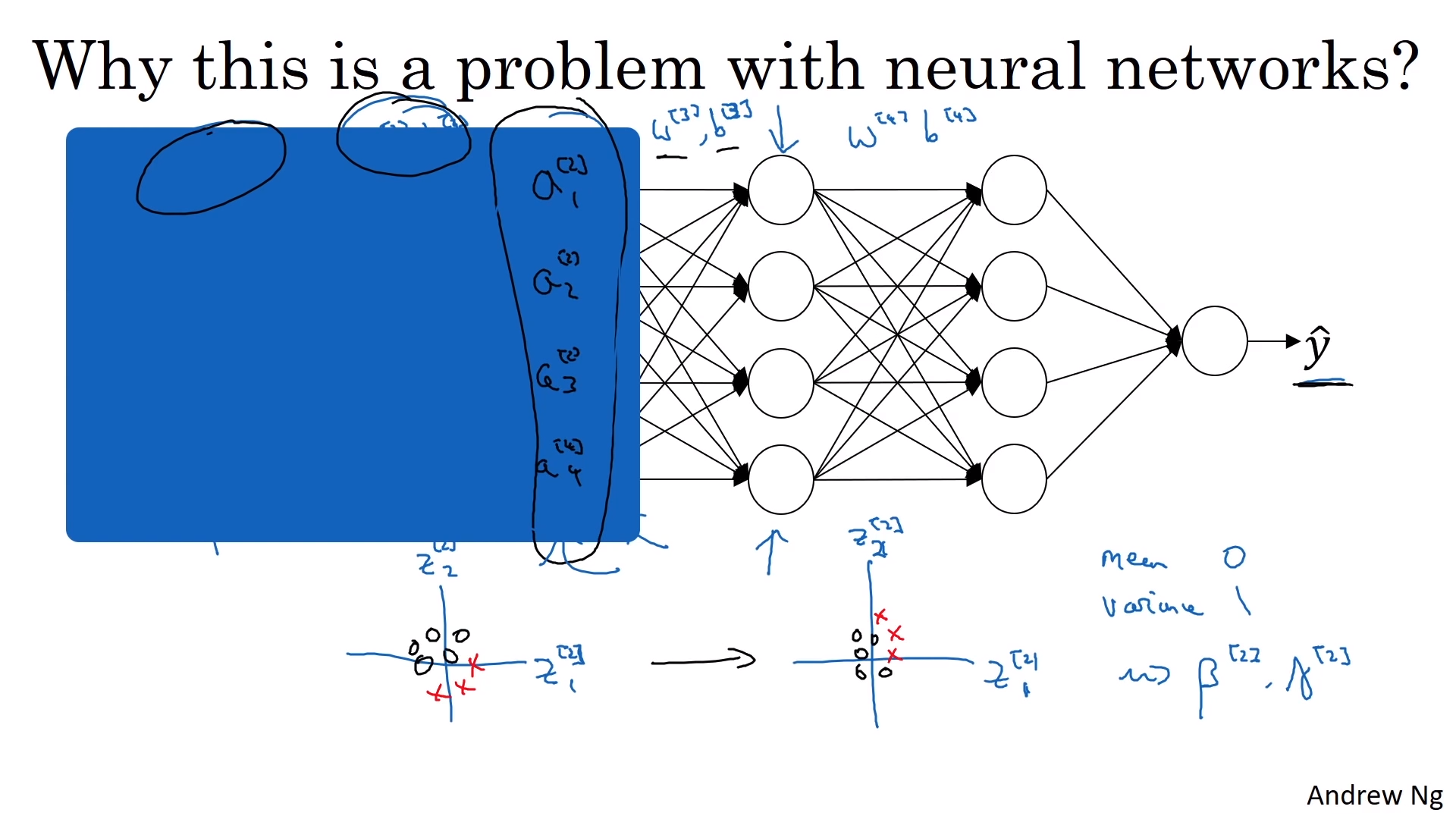
Batch norm은 은닉층 분포의 변화량을 줄여줌
앞선 층에서의 매개변수가 바뀌었을 때 다음 층이 받아서 학습하게 될 값을 제안하는 것(더 안정화)
앞 층의 매개변수와 뒤 층의 매개변수 간의 관계를 약화시킴
전체 신경망의 학습 속도를 향상시킬 수 있음
Regularization(일반화) 관점에서 Batch norm의 장점존재
- 각각의 minibatch에서 계산한 평균/분산 값은 잡음이 끼여 있음
- 드랍아웃은 곱셈 잡음을 가지고 있는 것으로 생각하면 좋음(*0 or *1 )
- Batch norm은 곱셈 잡음과 덧셈 잡음 둘다 존재함
- 즉 드롭아웃처럼 일반화 효과도 가지고 있음
- 은닉층이 하나의 은닉층에 너무 의존하지 않도록 함
- 그러나 미니배치 사이즈를 늘리면 노이즈 값도 줄어들기 때문에 배치 정규화를 일반화 목적으로 쓰는것은 적절치 않음
학습은 배치당 진행되지만 테스트는 데이터 각 한개마다 진행되므로 문제가 발생
- 각각 독립된 평균과 분산의 추정치를 사용하면 해결됨(여러 미치배치에 거쳐서 구한 지수가중평균(exponently weighted average)을 추정치로 사용)
- 각 상황에 대한 $\mu, \sigma^2$을 계산한 뒤 $z^{(i)}$,$\hat{z}^{(i)}$를 구하면 됨

여러 종류의 분류를 하는 문제
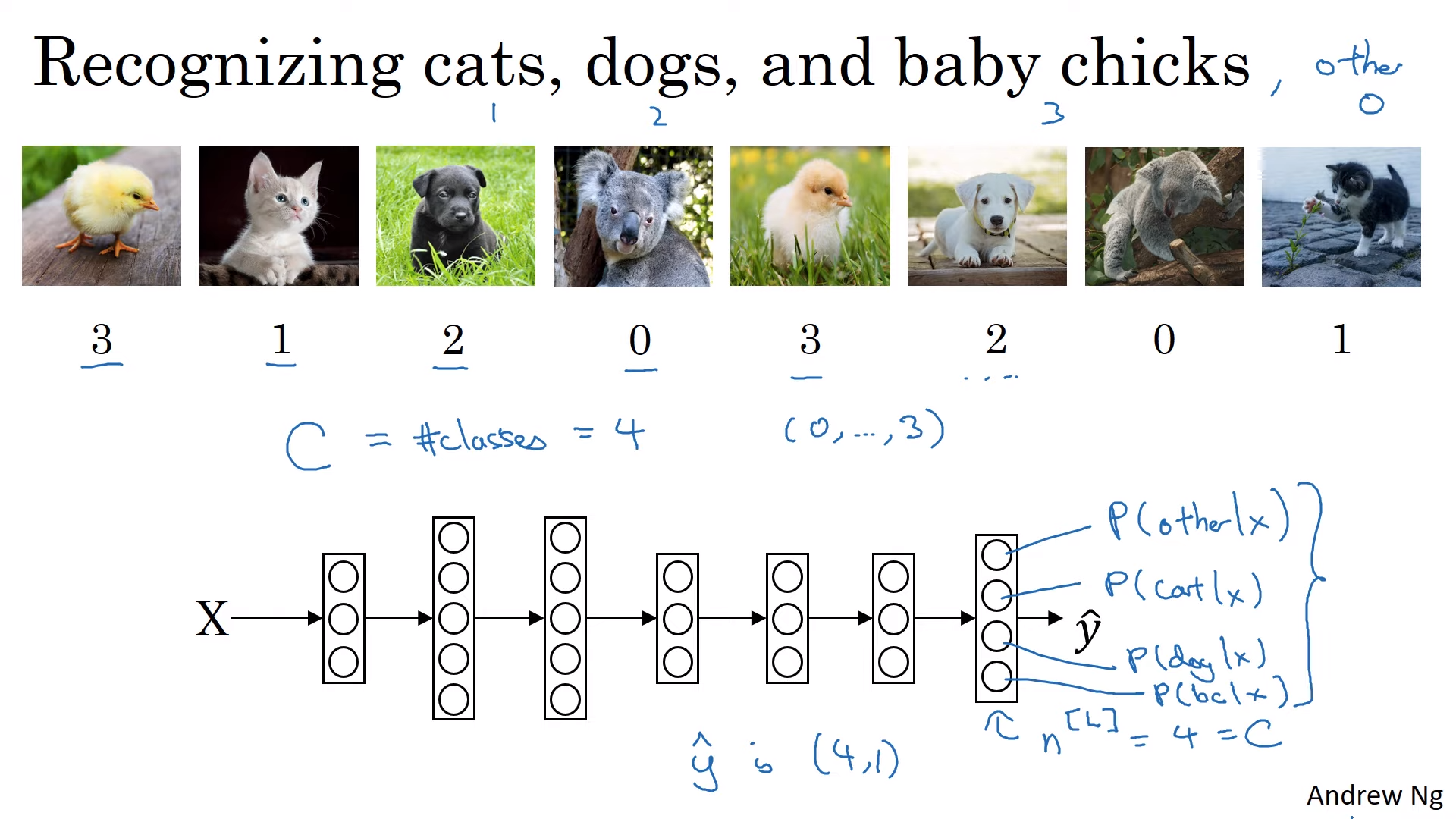
- 최종 적으로 분류 개수의 node가 나와야 함
- node의 값은 각각의 확률이 될 것임
- Softmax function 이용 $z^{[L]}=w^{[L]}a^{[L-1]}+b^{[L]}$ 에서 Activaton function으로 $t=e^{z^{[L]}}$ $a^{[L]}=\frac{e^{z^{[L]}}}{\sum_{j=1}^{4}{t_i}}$ 사용
- 활성화 함수가 (4,1)벡터를 받아서 (4,1) 벡터를 받음(입출력값이 벡터임)
- 이전 활성화 함수들은 모두 실수값을 반환했음
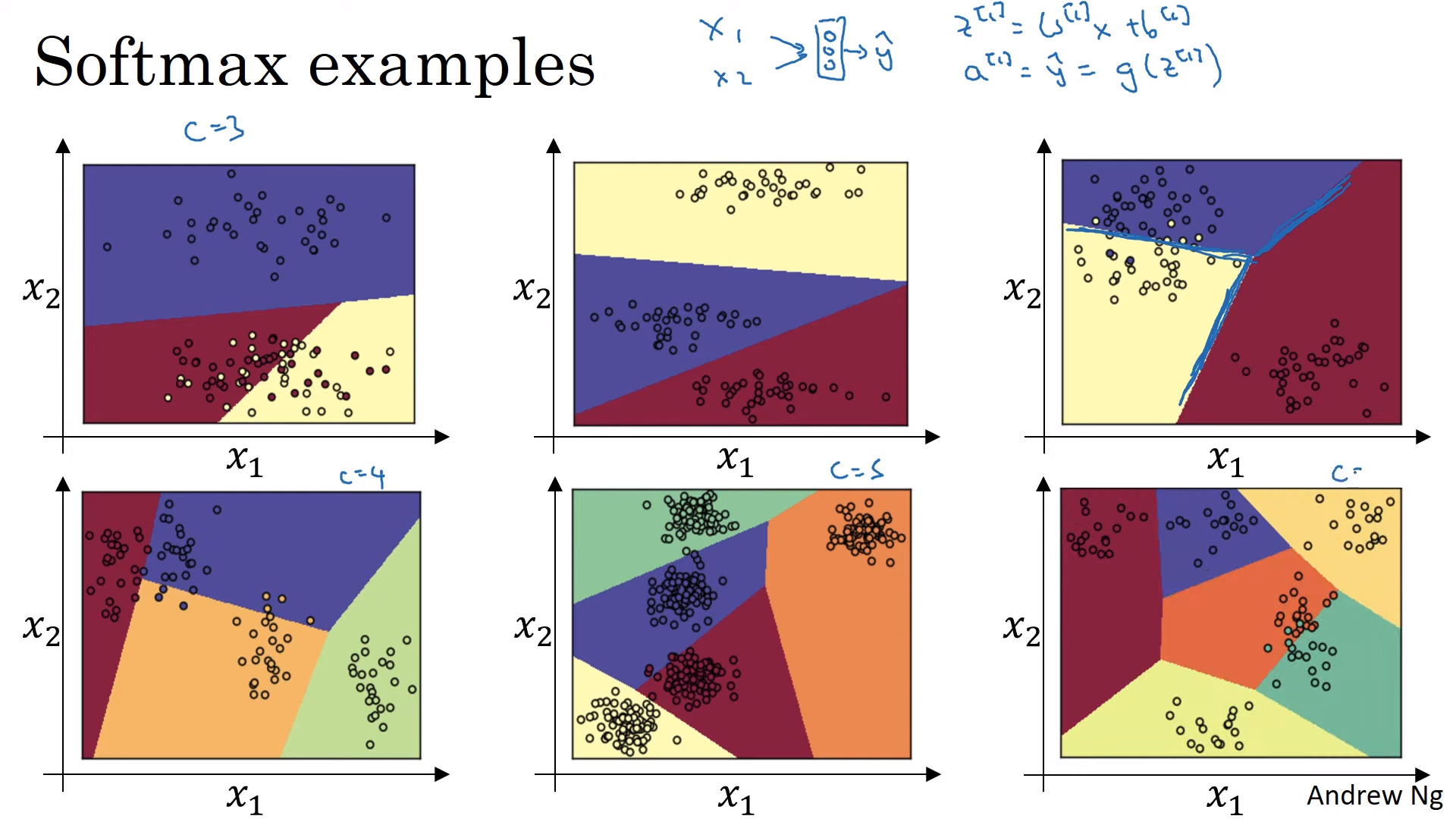
- 선형 경계선으로 나눔(linear boundary)
Hardmax
- softmax의 가장 큰 값을 1로 두고 작은 값들을 0으로 대응함
Logistic regression을 여러 class 분류로 확장시킨것
Loss function
- 관측에 따른 클래스가 뭐든 간에 해당 클래스에 대응되는 확률을 크게 만드는 것에 초점
- 통계학에서 최대 우도 함수랑 비슷함
Backprop
- $dz^{[L]}=\hat{y}-y$

과거에는 안좋은 local optimum에 빠지는 경우가 많았음
시간이 지나면서 지역 최적값에 대한 인식이 변화하게 됨
- 경사가 0인 점이 왼쪽 그림처럼 완전 지역 최적값이 아니고 대부분 인장점(saddle point)임
- 모든 차원에서 다 아래로 볼록한 경우는 거의 없기 때문이다.
Plateaus(인장 지역)
- 기울기가 0에 가까운 구역
- 학습을 많이 지연시킴
충분히 큰 신경망을 학습시키면 지역 최적값에 갇힐 일이 잘 없다
인장 지역은 학습 속도를 크게 감소시키는 구역이다.
모멘텀, RMSProp, Adam 과 같은 알고리즘이 성능을 높일 수 있다.