cs230_lec4_C2W2

(From : deeplearningai https://www.youtube.com/watch?time_continue=386&v=AwQHqWyHRpU)

Minibatch Gradient Descent

• 데이터의 개수가 엄청 클때 (m이 클 때 ) 경사하강법을 쓰기에는 시간이 오래 걸림
• Notation : $X^{{1} }$
• 전체 $X$ 데이터를 split 한 것
• 전체 프로세스는 다음과 같다.
• epoch: 훈련세트를 거치는 한 반복
• Gradient descent를 하면 각자 다른 미니배치에서 가져온 거라 노이즈가 있음(전체적으로는 감소함)
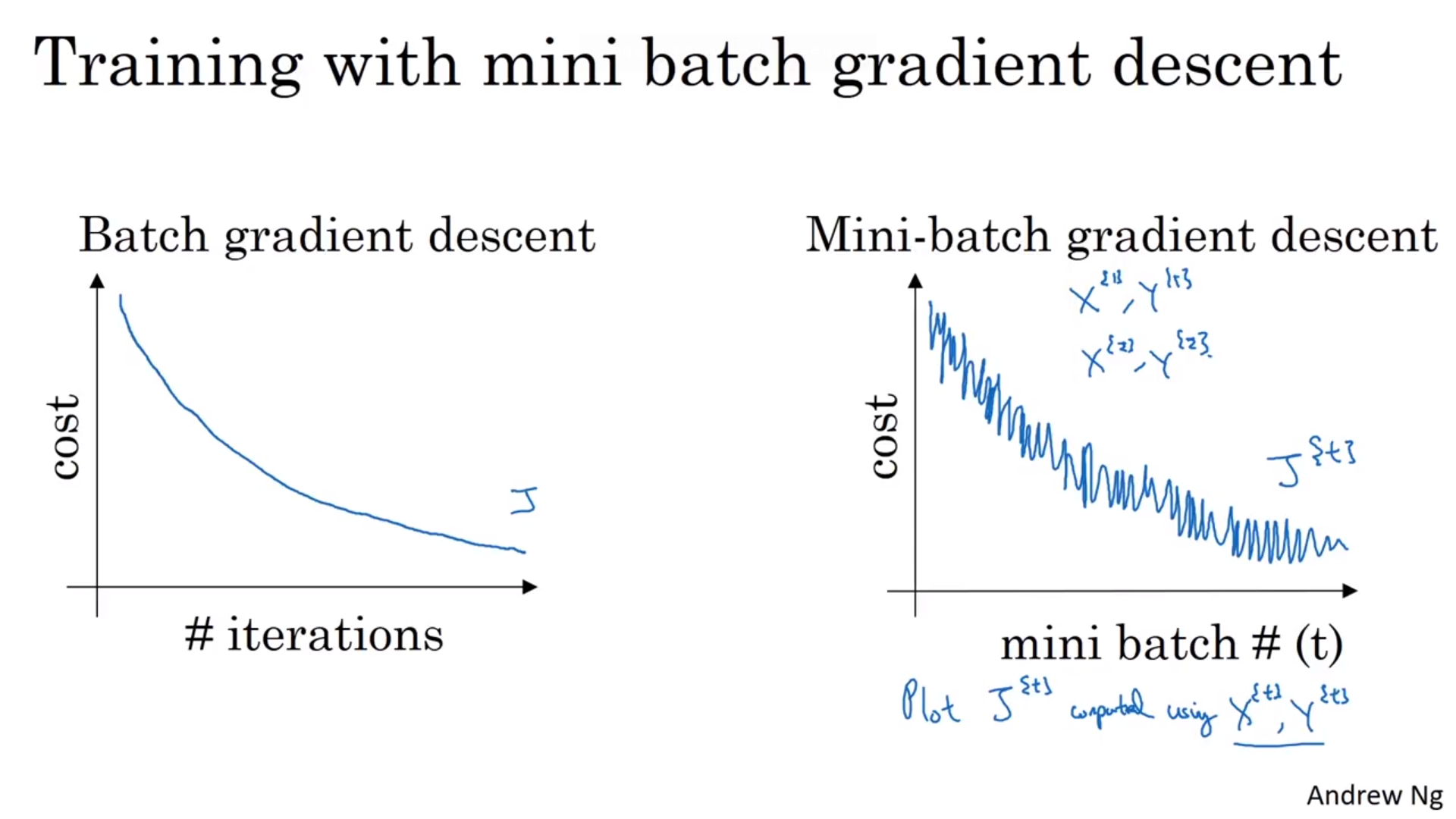
• 가장 극단적인 예
  • minibatch size=m : Batch Gradient Descent
    • 정확하지만 반복에 오래걸림
  • minibatch size=1 : Stochastic gradient descent
    • noise가 많을 수도 있지만 최솟값으로 곧바로 가진 않는다
    • Vectorization의 이점을 얻을 수 없다
  • 적절한 크기의 mimibath size
    • Vectorization 가능
    • 전체 훈련 세트가 진행되기를 기다리지 않고 진행가능
  • 그러면 적절한 크기의 minibatch size를 어떻게 설정할까?
    • Training set가 작다면(m $\leq$ 2000)) : batch gradient descent 사용하기
    • 일반적인 경우 : 64~512가 가장 일반적
    • 미니배치가 CPU/GPU 메모리에 맞는지 확인하기(아니라면 더 성능이 안좋아질 수 있음)

Exponentially weighted Average

$v_{t}=\beta v_{t-1} + (1-\beta)\theta_t$

• 일반적으로 $v_t$는 $\frac{1}{1-\beta}$날 동안의 온도의 평균과 동일함
• $\beta$가 커지면 이전 값들에 가중치를 더 주기 때문에 선이 더 smooth해짐

Bias correction

• 초기부분에 이전 데이터가 없어서 이동평균을 할 수 없음
• $\frac{v_t}{1-\beta^t}$ 이용

Gradient descent with Momentum

• 이동 평균을 통해 경사 하강법을 보다 부드럽게 만들어줌
• 편향보정은 잘 하지 않는데 왜냐하면 해당되는 반복 이후에 gradient descent가 잘 진행되기 때문
• 시작 전에 $V_{db},V_{dw}=0$으로 초기화해줘야 함
• 일반적으로는 $1-\beta$를 생략해서 씀
• 모멘텀이 없는 경사 하강법보다 일반적으로 잘 작동함
• 두가지 방식이 있는데 원래의 방식인 왼쪽 방식을 앤드류 옹은 더 선호함

RMSprop

• 경사하강법을 더 빠르게 하는 방법 중 하나
• 현재의 미니배치에 대해 dW,db 계산
• 진동을 줄이는 방식이라는 점에서 모멘텀과 비슷함
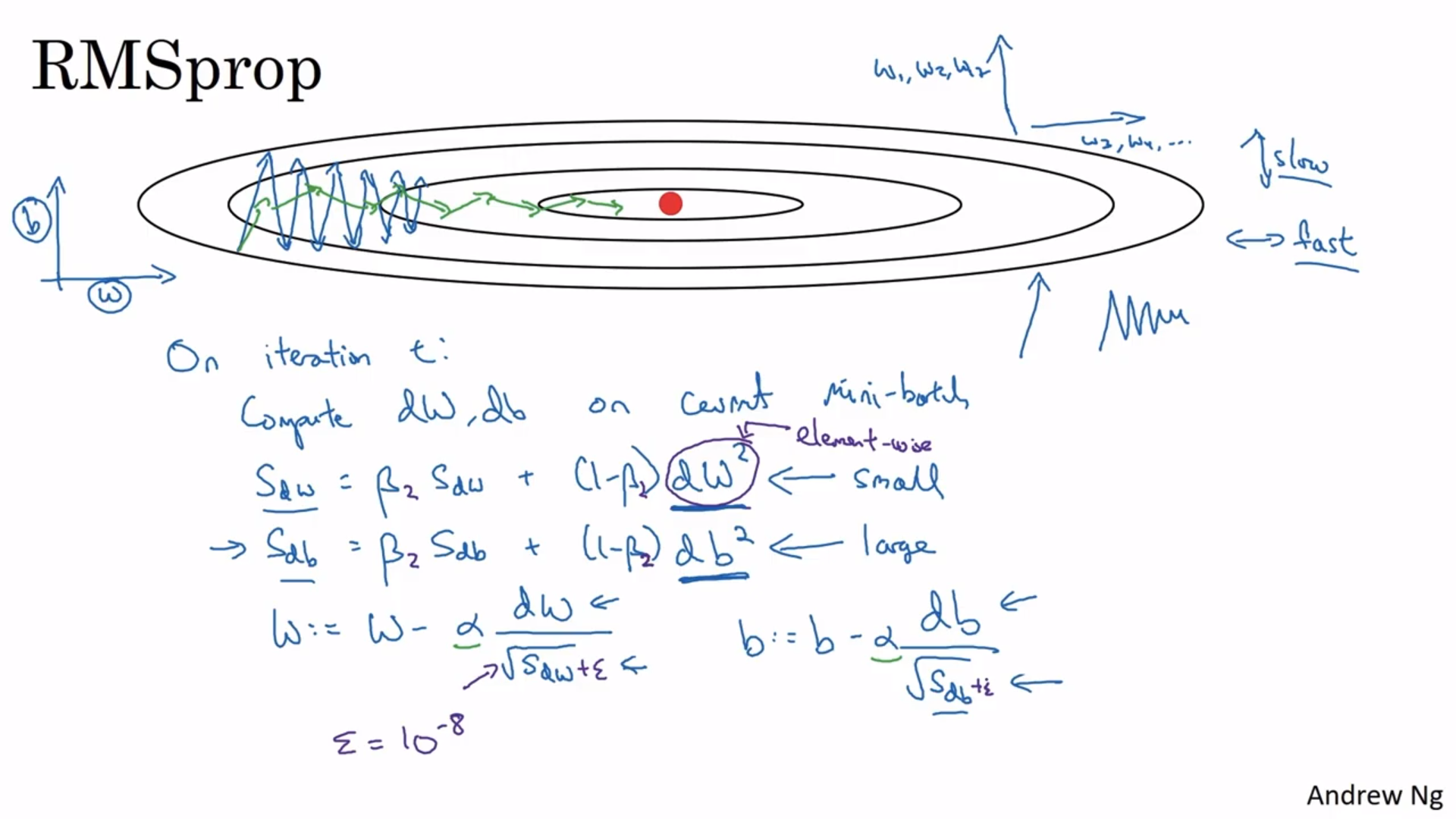
  • 큰 학습률을 사용해서 학습하지만 발산하지 않음
  • 제곱근을 0으로 나누지 않게 작은 값을 추가해 주기도 함($\epsilon$)
• 제프리 힌튼이 가르친 코세라 강의에서 나왔음

Adam 최적화 알고리즘

• Adaptive moment estimation
• 넓은 범위의 딥러닝 아키텍처에 잘 작동하는 알고리즘
• ‘RMSprop + 모멘텀’
• 저자가 추천하는 하이퍼파라미터 값
  • $\alpha$ : tuning해야 됨
  • $\beta_1(dw)$=0.9
  • $\beta_2(dw^2)$=0.99
  • $\epsilon$=10^{-8}

Learning rate decay

• noise가 있기 때문에 일정ㅎ란 learning rate 를 사용하면 해 근방에서 알고리즘 반복이 끝나질 않음
• $\alpha=\frac{1}{1+(decay-rate)*(epoch-num) }\alpha_0$
• Exponential decay : $\alpha=0.95^{epoch-num}\alpha_0$,
• Discrete staircase : $\alpha=\frac{1}{\sqrt}\alpha_0$
• Manual decay : 데이터 수가 적을때 가능