cs230_lec4_C2W1

(From : deeplearningai https://www.youtube.com/watch?time_continue=386&v=AwQHqWyHRpU)

Applied ML

• 정해주어야 할 것이 많음
• 위와 같은 사이클로 되어 있음

  Train/dev/test set

• 이전 세대에는 70/30, 60/20/20으로 나누는 것이 관행
• Big data 세대이므로 현재는 최대한 test,dev set을 줄이는 것이 관행
• 최근에는 일치하지 않는 훈련/ 테스트 분포에서 훈련시킨다
• 테스트 셋이 꼭 필요하지 않음(이런 Train/dev 셋을 Train/test 셋이라고 부르기도 함))

Bias, Variance

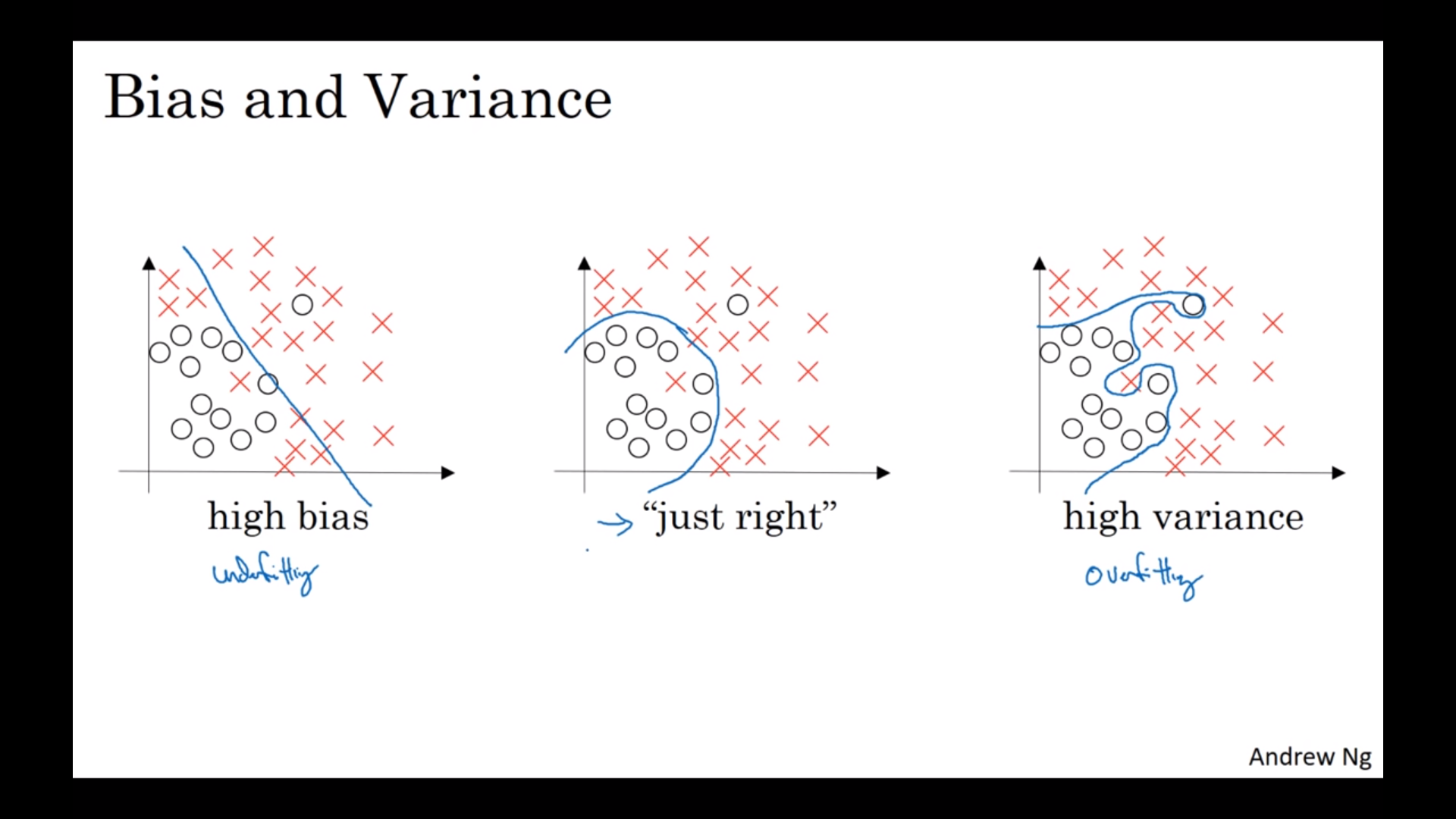
• Train/test error을 이용해서 high bias/variance 상태를 알 수 있다.
• Bayes error : 얻을 수 있는 최적의 오차
• 고차원에서는 어떤 부분에서는 high variance/bias 일 수 있지만 어떤 부분에는 아닐 수 있다.

Machine learning Recipe

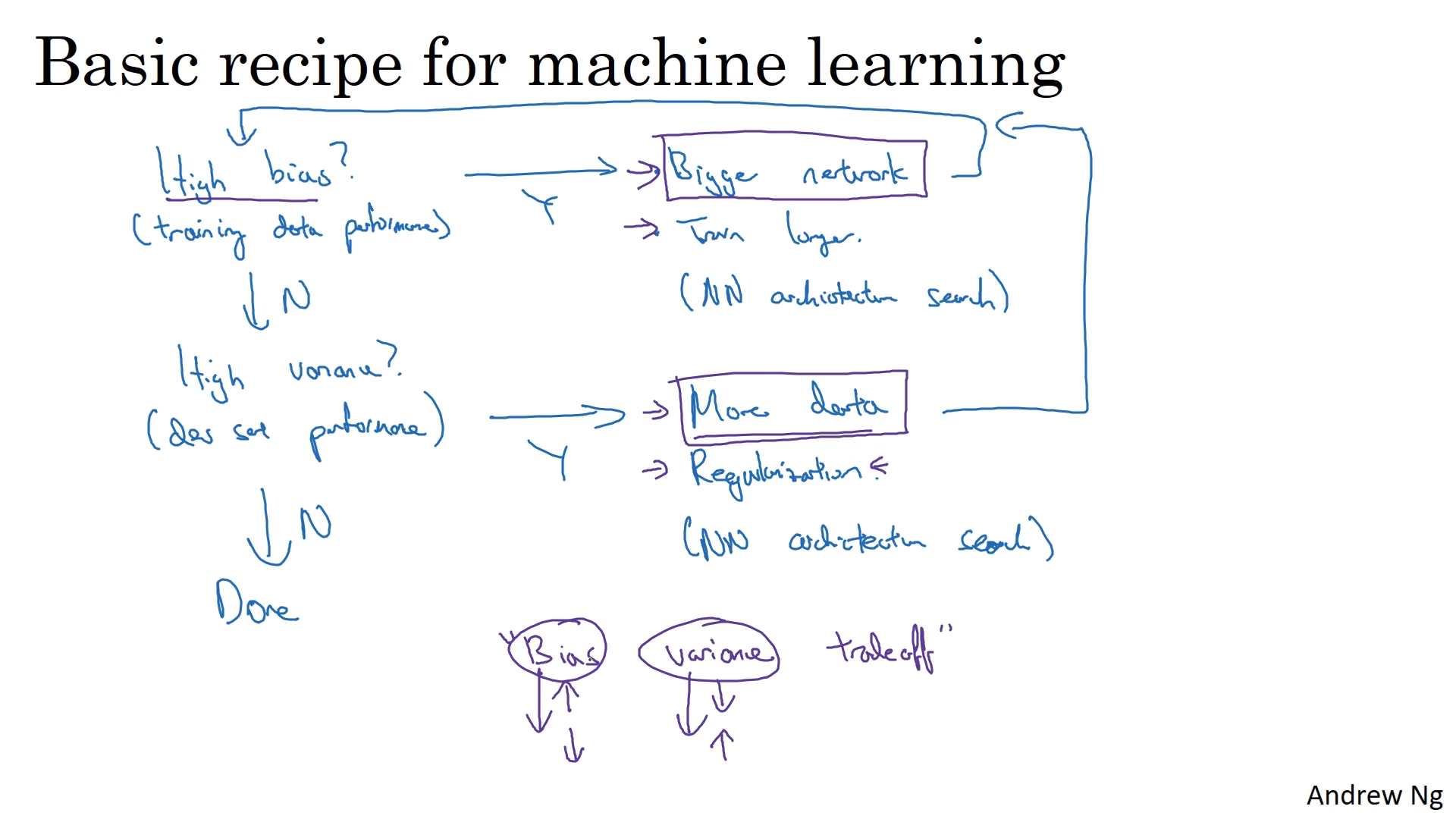
• 위의 순서대로 진행할 것
• 일반적으로 “Bias Variance Tradeoff”이 적용됨( 한쪽을 감소시키면 다른 한쪽이 증가함)
• Bigger Network/ More data는 한쪽만을 감소시킴
• Bigger Network는 계산이 복잡해진다는 것 이외론 항상 좋은 효과를 가져옴

정규화(Regularization)

• 과적합을 해결하는 한가지 방식
• 정규화 항을 추가하는 것
  • $\lambda$ : 정규화 상수

• L2 정규화
  • Frobenius norm 사용
  • 일반적으로 사용되는 방식
  • 끝에 정규화 항을 더해준 것 뿐이라 Weight Decay라 불리기도 함
• L1 정규화
  • w가 희소해짐->벡터 내부에 0 인 숫자가 많아짐
  • 모델 압축이 목표가 아닌 이상 많이 사용되지는 않음
• 정규화가 과적합을 해결하는 이유
  • 정규화 상수가 커지면 node의 weight가 0이 되는 경우가 많아짐
  • 그러면 모델이 더 단순한 모델로 변경됨
  • 정규화 상수에 따라서 Underfitting과 Overfitting을 오갈 수 있으므로 적절한 수를 고르는 것이 중요함
• tanh(x) 함수는 0 근방에서 기울기가 1에 가까움
• 경사함수가 단조감수할 수 있게 돕는다

드롭아웃(Dropout)

• 정규화 방식 중 하나
• 임의의 node를 정해서 없애고 학습하는 것
• 역 드랍아웃(Inverted Dropout)
  • 가장 보편적인 드랍아웃 기법
  • Illustrate with layer l=3, keep-prob=0.8
  • np.random.rand(a3.shape[0],a3.shape[1])< keep-prob
    • keep-prob 이하만 남긴다
  • a3=np.multiply(a3,d3) #a3*=d3
  • a3/=keep-prob
    • node를 없앨 때 a3의 기대값을 그대로 유지시키기 위해서 keep-prob로 나눠주는 것임
  • 테스트 시에는 드랍아웃을 하지 않음(noise만 증가시킬 뿐)
    • 예측을 하는 것이므로 결과가 무작위로 나오는 것은 원하지 않기 때문

• 드랍아웃이 잘 적용되는 원리

  1. node의 개수를 줄임으로써 더 작은 모델의 효과
  2. node가 임의로 없어지기 때문에 어떠한 한 특성에 의존할 수 없음. 즉 특정 node에 큰 가중치를 부여할 수 없기 때문에 가중치가 분산됨
• L2 정규화와 비슷한 효과지만 L2 정규화는 다른 가중치에서 적용된다는 점과 서로 다른 크기의 입력값에 더 잘 적응한 다는 점이 다름.
• node가 많은 층일수록 keep_prob을 낮게 해서 과적합을 방지하는 것이 좋음.
  • But 교차 검정을 위해 더 많은 하이퍼파라미터가 생길 수 있음
  • 즉 node 수가 많은 몇몇 층에서만 실시할 것
• 컴퓨터 비전쪽에서 성공적(픽셀 수가 많고, 데이터가 적어서 거의 대부분 과적합이 일어나기 때문에 사용함)
• 드롭아웃의 단점은 손실함수 J가 더이상 잘 정의가 안된다는 것
  • 반복할 때마다 임의의 node값을 없애기 때문에 모든 반복에서 잘 정의된 손실하수가 감소하는지 확인하기 어려움
  • 즉 디버깅하기 어려워짐

다른 정규화 방식

• Data Augmentation
  • 이미지를 뒤집어서 학습 셋에 추가하는 것
  • 이미지를 회전하고, 확대
  • 완전히 새 데이터보다 특성을 많이 추가해 주진 않지만 데이터를 따른 비용 없이 얻을 수 있는 방법임
• Early Stopping(조기종료)
  • Dev set error가 증가하기 전에 학습을 끝내는 것
  • 한번만 실행하면 되서 계산 비용이 작음
  • w는 작은 값으로 초기화 되기 때문에 신경망에서 반복을 계속 실시할 수록 w값이 증가함. L2 norm과 비슷하게 w값의 norm을 작게 만들기 때문에 신경망이 덜 과대적합하게 됨
  • 단 조기종료를 하면 손실함수 최적화와 과적합 방지 과정을 섞어서 두 문제에 대해서 독립적으로 작업하지 못하게 함
  • L2 정규화를 사용하면 이러한 단점을 해결할 수 있지만 정규화 매개변수에 많은 값을 대입해야 된 다는 점이 단점으로 작용(계산 비용이 많음)
• 알고리즘 학습할 때 중요한 Step들
  1. 손실함수 J를 최적화하기
     • 경사하강법, 모멘텀, Adam 등등
     • J(w,b)의 파라미터인 w와 b를 찾으면 됨
  2. 과적합하지 방지하기
     • 정규화, 조기종료 등등
     • 손실함수 최적화와 달리 여러가지를 고려해야 함
     • 분산을 줄이는 것과 유사-> 직교화라고 불림

데이터 정규화(최적화와 관련)

• 신경망의 훈련을 빠르게 할 수 있도록 도와줌
• 평균을 0으로 맞추고 분산을1로 맞춰줌
• 테스트 데이터에도 이전에 정규화 한 학습 평균, 학습 분 값으로 정규화해줘야 함

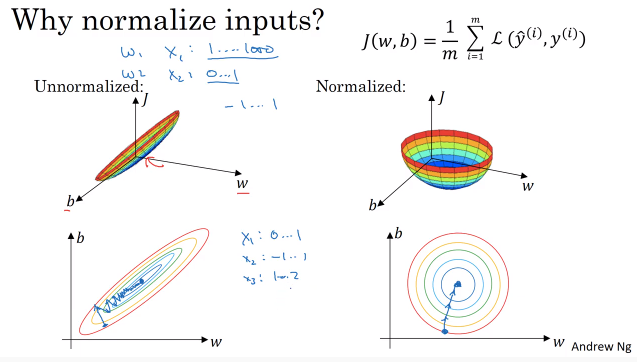
• 정규화를 하면 비용함수가 대칭적인 모양을 갖게 됨
• 원모양의 등고선일수록 왓다갔다 하지 않고 가운데로 바로 찾아갈 수 있기 때문에 step이 더 적게 걸림.

기울기 소실/폭발

• 매우 깊은 신경망을 훈련시킬때 경사가 기하급수적으로 작아질 수 있음
• 가중치 행렬의 성분을 1.5라고 잡고 그러한 신경망을 계속 거치게 된다면 가중치는 무한대로 폭발하게 될 것
• 가중치 행렬의 성분을 0.5라고 잡고 그러한 신경망을 계속 거치게 된다면 가중치는 0으로 수렴하게 될 것
• 경사하강법이 작동하기 어려워짐(특히 기울기 소실 시 학습하는 step이 매우 작아져서 학습이 오래걸림)
• 신경망 훈련의 큰 문제로 이전부터 작용했던 주제
• 부분적 해결이 가능

딥 러닝에서의 가중치 초기화

• 위의 기울기 소실 문제에 많은 도움을 주는 해결책
• w가 많아질수록 가중치를 나눠 갖는게 이득($z=w_1x_1+\cdots+w_nx_n$)
• 한가지 해결책은 분산을 $\frac{1}{n}$로 설정하는 것
• $w^{[l]}=np.rand.randn(shape)*np.sqrt(\frac{1}{n^{[l-1]}})$
• Relu일 경우 분산=$\frac{2}{n}$으로 $w^{[l]}=np.rand.randn(shape)*np.sqrt(\frac{2}{n^{[l-1]}})$ 가 더 잘 작동함
• $n^{[l-1]}$을 사용한 이유는 l층은 해당 층의 각 유닛에 대해서 그만큼의 입력을 받기 때문
• 각각의 가중치를 1보다 너무 차이 나지 않게 함으로써 소실/폭발 되지 않게 함
• Xavier initialization : tanh함수 사용시 $np.sqrt(\frac{2}{n^{[l-1]}})$ 대신에 $\sqrt{\frac{1}{n^{[l-1]}}}$ 사용
• $np.sqrt(\frac{2}{n^{[l-1]}})$ 대신에 $\sqrt{\frac{2}{n^{[l-1]}*n^{[l]}}}$ 사용

경사의 수치해석적 추정 방법

• 경사를 구할 때 한쪽만 사용하지 말고 양쪽 사용하는게 더 좋음
• $O(\epsilon)$ vs $O(\epsilon^2)$

경사 검사

• 역전파의 구현의 버그를 찾는데 도움이 되는 방법
• $W,b$를 Concatenate하여 $\theta$와 $d\theta$ 정의
• 수치해석 기법으로 $d\theta_{approx}$ 계산
• 원래 값과 차이(Euclidian distance)를 계산
  • 작은 값이 나오면 구현이 잘 된 것이며, 큰 값이 나오면 버그를 의심해 볼 필요가 있음

• 조심해야 할 점들

  (1) 너무 오래 걸리기 때문, 디버그 할 때만 체크하고 학습 돌리는 데는 꺼야 함

  (2) 거리차이가 많이 발생할 때 각 컴퍼턴넌트 $W,b$ 값을 확인해서 어디서 버그가 발생했는지 확인하기

  (3) 정규화항이 $\theta$에 포함되어 있는 것을 까먹지 말기

  (4) 매 실행마다 Dropout 이 은닉 유닛의 부분집합을 삭제하기 때문에 계산하기 쉬운 방법은 없음. 따라서 Grad check 할 때에는 Dropout없이 사용한 뒤에 이후 Dropout 실행.

  (5) Random initialization 실행 후 사용하기. w,b값이 0이 실제로 가까운데도 실행하면 값이 커질 수 있기 때문