신호 및 시스템 Chapt 4

Alan V. Oppenheim, Signals and Systems 책 내용입니다. 앞으로는 내용의 핵심만 정리할 예정

연속시간 푸리에 변환

4.0 서론

• 앞서서는 주기 신호에 대해서만 복소지수 함수의 선형 경합으로 표현하였지만 이 장과 다음 장에서는 이 개념을 비주기 신호 로 확대
• 주기 신호에는 복소지수의 구성 요소들이 고조파 형태로 연관, 비주기 신호에는 주파수 영역에서 구성 요소들이 무한하게 가까움

4.1 비주기 신호의 표현: 연속시간의 푸리에 변환

4.1.1 비주기 신호의 푸리에 변환 표현의 전개

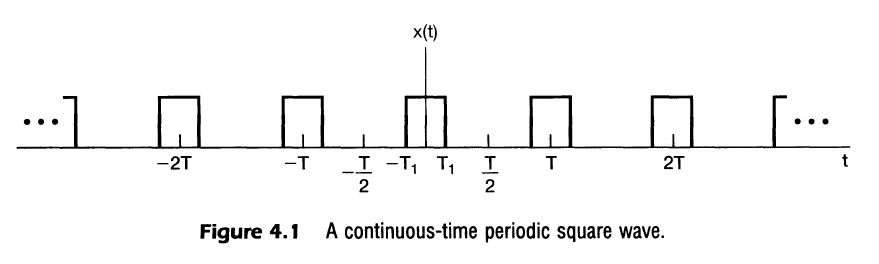
• 위에 해당되는 일반적인 형태의 구형파의 계수는 다음과 같음

$$a_k=\frac{2sin(k_{w_0}T_1)}{kw_0T}$$

• 이를 포락선 함수(Contour Function) 의 샘플로도 해석 가능

$$Ta_k=\frac{2sinwT_1}{w}|_{w=kw_0}$$

• 위는 $T_1$이 고정되었을 때 $T_1$에 따른 푸리에 계수를 의미
• T가 증가함에 따라, 즉 기본주파수 $w_0=2\pi/T$가 감소함에 따라 포락선은 더 가까운 간격으로 샘플링됨

• 즉 푸리에 계수의 집합은 T가 무한대로 갈 때 포락선 함수에 근접하게 됨

• 아래 예시 또한 T를 무한대로 증가하면 주기 신호가 비주기 신호로 가까워진다는 것을 나타냄

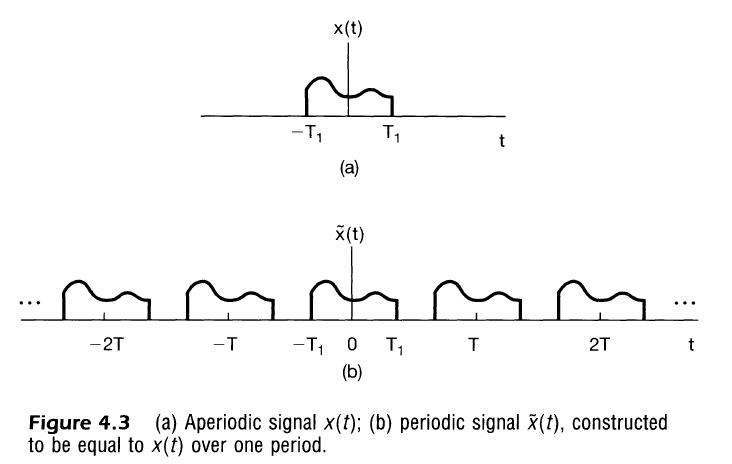
• 포락선$X(jkw_0)=Ta_k$을 새로운 변환으로 정리하면 다음과 같이 정리됨을 확인 가능

$$x(t)=\frac{1}{2\pi}\int_{-\infty}^{\infty}X(jw)e^{-jwt}dt$$ $$X(jw)=\int_{-\infty}^{\infty}x(t)e^{-jwt}dt$$

• 함수 $X(jw)$는 $x(t)$의 푸리에 변환(Fourier Transform) 또는 적분 이라고 불리며 즉 맨 위의 식은 푸리에 역변환식 으로 불린다
• 푸리에 계수가 $x(t)$의 한 주기에 대한 푸리에 변환 결과의 샘플링에 비례하기 때문에 다음 관계식도 유도 가능

$$a_k=\frac{1}{T}X(jw)|_{w=kw_0}$$

4.1.2 푸리에 변환의 수렴

• 위의 유도식은 임의의 x(t)가 유한한 시간 구간에 존재한다고 가젛하였지만 무한한 시간구간에 존재하는 신호들에 대해서도 유효함
• 증명은 원래의 신호 $x(t)$와 푸리에 역변환 식으로 구한 $\hat{x}(t)$사이의 오차의 에너지값이 0에 도달하는지에 따라 결정됨
• 주기신호처럼 불연속점을 제외하고 어떤 t 값에 대해서도 해서도 $\hat{x}(t), x(t)$가 같다는 것을 보장하기 위한 충분조건들의 집합은 아래와 같음

Drichlet 조건

1. x(t)의 절대값은 적분 가능하다
2. x(t)의 어떤 유한한 구간에서 한정된 수의 최대값과 최소값을 갖느다
3. x(t)는 어떤 유한한 구간에서 한정된 ㅜㅅ의 불연속점을 갖는다. 각각의 불연속점은 반드시 유한한 값을 가져야 한다

• 다음절(4.2)에서는 임펄스 함수가 푸리에 변환에서 허용되는 경우, 절대값과 절대값의 제곱이 적분이 안되는 주기함수 또한 푸리에 적분이 가능하다는 것을 배울 것!

4.1.3 연속 푸리에 변환의 예들

• 구형파를 변환시키면 특정 $(sina\theta)/b\theta$ 형태의 함수와 직각함수로 이루어짐, 반대로 푸리에 변환값이 구형파일 때도 역변환 값이 해당 함수꼴로 나타남 (쌍대성 원칙(Duality Property)의 예)
• 이러한 꼴의 함수를 sinc 함수라고 불리며 푸리에 분석과 LTI 시스템에 빈번하게 사용된다

$$sinc(\theta)=\frac{sin\pi \theta}{\pi\theta}$$

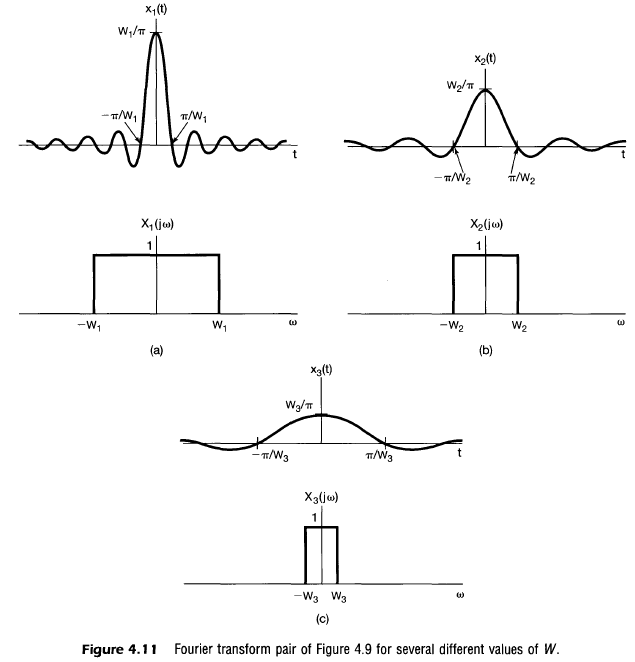
• W가 증가할수록 X(jw)가 더 넓어지고 t=0일때 x(t)의 최대값은 더 높아지고 첫번째 로브의 폭은 더 좁아지게 됨

• 반대의 경우도 성립

4.2 주기 신호의 푸리에 변환

• 주기 신호와 비주기 신호가 같은 틀에 논의될 수 있게 하도록 함
• 단위 임펄스를 도입해서 유도해보면 3장에서 봤던 푸리에 급수 표현을 얻을 수 있음(책 참고)
• 주기 신호의 푸리에 변환은 고조파 주파수에서 발생하는 임펄스 열로 표현 가능

4.3 연속시간 푸리에 변환의 성질

• 기본 관계를 다음과 같이 정의하자

$$x(t) \leftrightarrow X(jw)$$ $$y(t) \leftrightarrow Y(jw)$$

4.3.1 선형성

$ax(t)+by(t) \leftrightarrow aX(jw)+bY(jw)$

4.3.2 시간이동

• 시간이동의 성질 중 하나는 이동된 푸리에 변환값의 크기가 변하지 않는다는 점

$$x(t-t_0) \leftrightarrow e^{-jwt_0}X(jw)$$

4.3.3 켤레 대칭(Conjugate Symmetry)

$$x*(t) \leftrightarrow X*(-jw)$$

• x(t)가 대칭이면 켤레대칭의 성질을 가짐

$$X(-jw)=X*(jw)$$ $$X*(-jw)=X(jw)$$

• 실수값의 푸리에 변환을 게산하거나 표현해 줄 때는 변환 겨과의 실수와 허수부분 또는 크기와 위상 부분을 양의 주파수 값에만 한정하는 것 이 필요
• 실수함수 $x(t)=x_e(t)+x_o(t)$에 대해서 다음과 같은 결론을 얻을 수 있음

$$x(t) \leftrightarrow X(jw)$$ $$x_e(t) \leftrightarrow Re(X(jw))$$ $$x_o(t) \leftrightarrow Im(X(jw))$$

4.3.4 미분과 적분

$$\frac{dx(t)}{dt} \leftrightarrow jwX(jw)$$ $$\int_{-\infty}^t x(\tau)d\tau \leftrightarrow \frac{1}{jw}X(jw)+\pi X(0)\delta(w)$$

4.3.5 시간과 주파수 스케일링

$$x(at) \leftrightarrow \frac{1}{|a|}X(jw/a)$$

• 이중에서 a=-1일때 많이 사용됨

$$x(-t) \leftrightarrow X(-jw)$$

4.3.6 쌍대성(Duality)

• 역변환 관계가 형식에 있어서는 유사하지만 완전히 같지 않은 것이 성질로 이어짐
• 책에 몇몇 예시가 있으니 앞의 성질들과 비교하면서 이해

4.3.7 파시발 정리(Parseval’s Relation)

$$\int_{-\infty}^{\infty}|X(t)|^2 = \frac{1}{2\pi}\int_{-\infty}^{\infty}|X(jw)|^2dw$$

• 신호의 단위시간당 에너지를 모든 시간에 대해 적분한 것은 단위주파수당 에너지를 모든 주파수에 대해 적분하는 것과 같다는 의미

• 여기서 $

  X(jw)^2

  $는 에너지 미로 스펙트럼 이라 불림

• 앞서서 배운 주기적 신호에 대한 파시발 정리와 직접적으로 관계됨

4.4 컨볼루션 성질

• 3장과 동일하게 LTI 시스템의 응답 즉 입력과 시스템의 컨볼루션도 푸리에 변환의 곱으로 표현됨

$$y(t)=h(t)*x(t) \leftrightarrow Y(jw)=H(jw)X(jw)$$

• 필터링과 많은 시스템 응용에서 많이 사용됨

• 컨볼루션의 성질에 의해 cascade한 시스템 순서 변환 가능
• LTI 시스템이 안정하다면 임펄스 응답의 절대값이 적분 가능하므로 다음의 식이 성립

$$\int_{-\infty}^{\infty} |h(t)|dt < \infty$$

• 또 이는 앞서 공부한 디히리트(Dirichlet) 조건 중 하나이므로 나머지 두 개의 조건이 성립할 때 안정적인 LTI 시스템은 주파수 응답 $H(jw)$를 가지고 있다는 것을 알 수 있음

• 즉 불안정한 LTI 시스템을 검사하는 목적으로 연속시간 푸리에 변환을 일반화 할 수 있으며 이는 라플라스 변환(Laplace Transform) 이며 9장에서 논의한다.

• 예제 4.18에서 필터 설계에 관한 문제점을 다룸
  • 이상적인 저역통과 필터가 완벽한 주파수 선택 특성을 갖는 반면, 임펄스 응답은 바람직하지 않은 몇가지 특징들을 가짐
    1. t가 0봗 작을때 h(t)가 0이 아니기 대문에 이상적인 저역토오가 필터는 인과성을 가지지 않음
    2. 이상화된 필터는 근사화가 어렵다(6장에서 논의)

• 더 쉽게 구현될 수 있는 비이상적 필터가 많이 사용됨. 구현의 용이성 및 주파수 선택특성과 시간 영역에서 진동특성 들 간의 균형적인 고려가 가능하기 때문

• 컨볼루션 성질은 컨볼루션 적분을 계산할 때 유용함

4.5 곱셈 성질

• 쌍대성(Duality)에 의해 시간 영역에서의 곱셈은 주파수 영여에서의 컨볼루션과 일치

$$r(t)=s(t)p(t) \leftrightarrow R(jw)=\frac{1}{2\pi}\int_{-\infty}^{\infty} S(j\theta)P(j(w-\theta))d\theta$$

• 하나의 신호에 다른 신호를 곱하는 것은 신호의 크기를 조절하거나 변조(modulate) 하는 것으로 생각할 수 있음. 결과 두 신호의 곱은 진폭 변조(Amplitude modulation) 이라고 불림
• 즉 위의 성질은 종종 변조 성질이라고도 불림
• 7,8장에서 추가로 논의될 예쩡

4.5.1 가변주파수를 갖는 주파수 선택적인 필터링

• 앞서 말한 것과 같이 곱셈성질은 1) 통신 시스템의 진폭 변조, 2) 선택적 대역통과 필터 구현에 많이 이용됨
• 중심 주파수는 전력변환장치에서 다수의 소자 값에 의해 결정
• 중심 주파수를 변경하기 위해서는 이러한 값들이 동시에 정확한 방법으로 조절되어야 하고 이는 고정된 필터를 만드는 것보다 더 어려움
• 필터특성을 직접적으로 변경시키는 것에 대한 대안으로 고정된 특성의 주파수선택적 필터를 사용하고 정현파 직폭 변조 이론을 이용하여 신호의 스펙트럼을 적절하게 이동하는 방법이 사용됨

$$F(jw)=W(j(w+w_0))$$

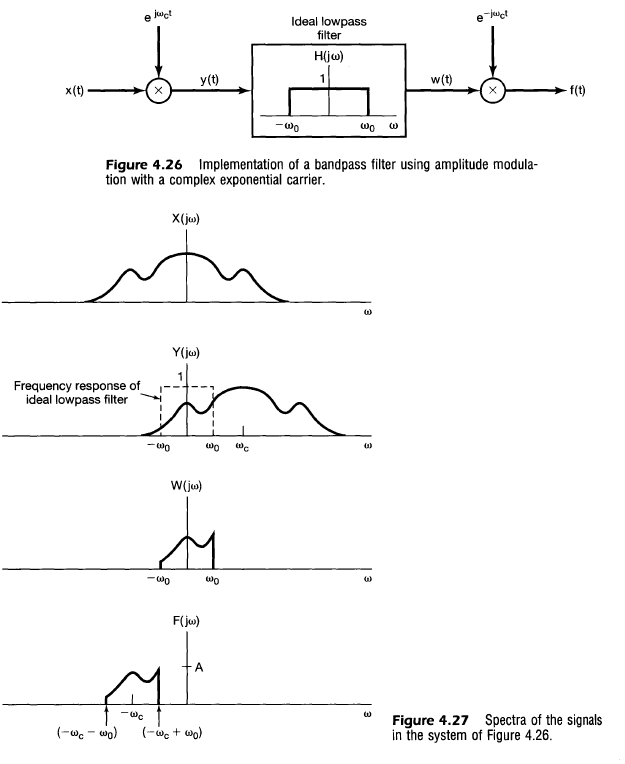
4.6 푸리에 성질과 기본적인 푸리에 변환 쌍을 위한 표

4.7 선형 상수계수 미분방정식에 의한 시스템

• 연속시간 LTI 시스템은 입력과 출력이 선형 상수계쑤 미분방정식을 만족하고 형태는 아래와 같다

$$\sum_{k=0}^{N} a_k\frac{d^ky(t)}{dt^k}=\sum_{k=0}^M b_k\frac{d^kx(t)}{dt^k}$$

• 따라서 주파수 응답은 다음과 같이 구할 수 있음

$$H(jw)=\frac{Y(jw)}{X(jw)}=\frac{\sum_{k=0}^M b_k(jw)^k}{\sum_{k=0}^N a_k(jw)^k}$$

• 즉 LTI 시스템에 관련된 문제를 단순한 대수학적 문제로 다눗ㄴ화 할 수 있음

4.8 요약

• 푸리에 변환들은 다양한 범위의 중요한 성질들을 가지고 있는데 가장 중요한 것은 컨볼루션, 곱셈 성질임
  • 컨볼루션 성질은 복소지수 신호의 고유함수 성질의 직접적인 결과, LTI 시스템의 주파수 영역 분석에 중요한 역활을 함
  • 곱셈 설질은 샘플링과 변조 시스템의 주파수 영역 분석 기반을 제공