신호 및 시스템 Chapt 3

Alan V. Oppenheim, Signals and Systems 책 내용입니다. 앞으로는 내용의 핵심만 정리할 예정

주기신호의 푸리에 급수표현

3.0 서론

• 앞에서 일반적인 신호를 선형 임펄스의 선형결합으로 표현한 것과 같이 이번 장에서는 주기신호를 주기적인 복소지수들의 결합으로 표현할 예쩡

3.1 역사

• 오일러는 LTI시스템을 해석하는데 유용한 삼각함수 합의 특성중 하나를 유도
• 푸리에는 모든 주기적인 신호를 정현파의 합으로 표현 가능하다고 주장
• 이후 Drichlet에 의해서 푸리에 급수로 표현될 수 있는 정확한 조건들이 제시됨
• 공학, 수학, 과학 등등 여러 분야에 많이 활용됨
• 이산신호, 연속 신호 각각 독자적으로 분야가 발전되어 오는중
• FFT(고속 푸리에 변환) 알고리즘을 통해 계산 시간 감소

3.2 복소지수에 대한 LTI 시스템의 응답

• LTI 시스템을 공부하는데 신호를 다음 두 가지 성질을 갖는 기본 신호의 선형결합으로 표시하는 것이 편리

  1) 기본 신호들은 광법위한고 유용한 종류의 신호를 만드는데 사용할 수 있어야 함 2) 각 기본신호에 대한 LTI 시스템의 응답은 이러한 기본 신호들의 선형응답으로 이루어진 어떤 신호에 대한 시스템의 응답이 편리하게 표시될 수 있도록 구조상 간단해야 함

• 푸리에 해석에서는 이러한 두 특성이 연속,이산 시간에서 복소지수함수 로 주어짐
• 복소지수함수 : s와 z가 복소수일때 각각 $e^{st}$(연속 시간), $z^n$(이산 시간)의 형태로 주어짐
• LTI 시스템에서 복소지수의 응답이 단지 진폭만 변화할 뿐 같은 복소지수를 가짐

$$연속시간 : e^{st} \rightarrow H(s)e^{st}$$ $$이산시간 : z^n \rightarrow H(z)z^n$$

• 여기서 진폭항 $H(s),H(z)$는 고유치(eigenvalue) 라고 불리며 시스템의 출력이 각 신호의 상수(복소상수)배가 되는 신호를 시스템의 고유함수(eigenfunction)이라 함
• 아래 식 유도는 책 참고할 것

$$H(s)=\int_{-\infty}^{+\infty}h(\tau)e^{-s\tau}d\tau$$ $$H(z)=\sum_{k=-\infty}^{+\infty}h[k]z^{-k}$$

• 즉 입력 신호가 복소지수 형태이면 시스템의 응답을 다음과 같이 표현 가능

  3.3 연속시간 주기 신호의 푸리에 급수 표현

  3.3.1 조화적으로 관련된 복소지수의 선형결합

• 주기신호란 모든 t에 대해 양의 T값에 대해 다음의 성질을 성립하는 신호

$$x(t)=x(t+T)$$

• 복소지수를 사용해서 다음과 같이 주기신호를 나타낼 수 있음

$$x(t)=\sum_{k=-\infty}^{\infty}a_ke^{jkw_0t}$$

• 이와 같이 주기신호를 표시하는 것을 푸리에 급수 표현법 이라고 부름
• x(t)가 실수일 경우 $x*(t)=x(t)$ 이므로 다음과 같이 수정 가능
  • 방법 1. $a_k=A_ke^{j\theta}$ 로 가정할 때

$$x(t)=a_0+\sum_{k=-\infty}^{\infty}[a_ke^{jkw_0t}+a_{-k}e^{-jkw_0t}]=a_0+2\sum_{k=-\infty}^{\infty}A_kcos(kw_0t+\theta_k)$$

• 방법 2. $a_k=B_k+jC_k$ 로 가정할 때

$$x(t)=a_0+\sum_{k=-\infty}^{\infty}[a_ke^{jkw_0t}+a_{-k}e^{-jkw_0t}]=a_0+2\sum_{k=-\infty}^{\infty}B_kcos(kw_0t)-C_kcos(kw_0t)$$

3.3.2 연속시간 주기 신호의 푸리에 급수 표현의 결정

• 식 정리 방식은 책에 잘 나와있음
• 결론적으로 다음의 식이 성립

$$a_n=\frac{1}{T}\int_{-\infty}^{\infty}x(t)e^{jnw_0t}dt$$

• 위의 식을 분해식(analysis equation) 이라고 하며, 아래의 기존 식을 합성식(synthesis equation) 이라고 한다
• $a_k$를 푸리에 급수 계수(coefficient) 또는 스펙트럼 계수 라고 불리운다
• 식을 통해 확인할 수 있듯이 $a_0$은 $x(t)$의 한 주기 동안의 평균과 같음

3.4 푸리에 급수의 컨볼루션

• 그렇다면 실제 모든 주기 신호가 푸리에 급수로 표시할 수 있을까??
• 한 주기의 오차에 대한 에너지 정의

$$E_N=\int_T |e_N(t)|^2 dt$$

• 신호의 유한급수의 합 함수 정의

$$x(t)=\sum_{k=-N}^{N}a_ke^{jkw_0t}$$

• 이를 최대화 하는계수

$$a_k=\frac{1}{T}\int_{-\infty}^{\infty}x(t)e^{jkw_0t}dt$$

• 즉 푸리에 계수 결정하는 방식과 같으므로 최선의 근사화는 푸리에 급수를 원하는 수의 항 만큼 취하고 나머지를 버리는 것
• 그러나 $x(t)$에 따라서 특정 $a_k$가 발산가능 + 모든 계수가 유한하더라도 무한급수가 $x(t)$에 수렴하지 않을 수 있음
• 다행히도 많은 종류의 주기 신호에 대해 문제 없음 + 일부 불연속 신호에도 적용 가능
• 푸리에 급수로 표현 가능한 주기신호의 한 종류는 한 주기 동안 유한한 에너지를 갖는 신호들 $\rightarrow$ 푸리의 급수와 실제 $x(t)$값은 동일하지 않으나 에너지 차이는 0임
• 아래의 Drichlet 조건에 만족하는 신호들은 불연속한 t 값을 제외한 곳에서의 푸리에 급수와 같음
  • Drichlet 조건 1. 어떠한 주기에서도 x(t)의 절대치는 적분가능해야 한다 $\rightarrow$ 위 식은 계수가 유한하다는 것을 증명
  $$\int_T |x(t)|dt<\infty$$
  • Drichlet 조건 2. 어떠한 유한 시간영역에서 x(t)는 제한된 변동폭을 갖는다. 즉 유한개의 극대, 극소값을 가져야 함
  • Drichlet 조건 3. 어떠한 유한 시간영역에서 불연속점이 유한개여야 함
• 즉 연속적인 신호들은 푸리에 변환 값이 원래 신호와 같음
• 유한 불연속점을 갖는 신호와 푸리에 변환 신호는 에너지의 차이가 0이기 때문에 실용적 관점에서 같다고 봄
• 불연속 적인 신호들은 몇몇 점들에서만 다르기 때문에 원래 신호와 푸리에 변환한 신호 컨볼루션 내 적분값은 동일
• 즉 특정 점들을 제외하고 적분값이 같기 때문에 컨볼루션에서 동일한 역활 $\rightarrow$ LTI 시스템에서 두 신호를 동일하다고 볼 수 있음
• Gibbs 현상 (Gibbs phenomenon) : 불연속 신호의 불연속점 가까이 고주파 맥동과 초과치(overshoot)가 발생하며 N개의 푸리에 급수 근사법을 사용하기 위해서는 맥동의 총 에너지가 무시될 만한 큰 N값을 선택해야 한다는 것

3.5 연속시간 푸리에 급수의 특성

• 많은 신호들을 푸리에 급수로 전개하는데 있어서 복잡성 감소의 도움을 줌
• 기본 관계를 아래와 같이 정의하자

$$x(t) \leftrightarrow a_k$$ $$y(t) \leftrightarrow b_k$$

3.5.1 선형성(Linearity)

$$z(t))=Ax(t)+By(t) \leftrightarrow c_k=Aa_k++Bb_k$$

3.5.2 시간 변위(Time shifting)

$$x(t-t_0) \leftrightarrow e^{-jkw_0t_0}a_k$$

3.5.3 시간 반전(Time reversal)

$$x(-t) \leftrightarrow a_{-k}$$

3.5.4 시간 배율(Time scaling)

• 계수들은 변화 없음
• 기본 주파수만 변화함

$$x(\alpha t)=\sum_{k=-\infty}^{\infty}a_ke^{jk(\alpha w_0)t}$$

3.5.5 곱셈

$$x(t)y(t) \leftrightarrow h_k=\sum_{l=-\infty}^{\infty}a_lb_{k-l}$$

3.5.6 공액과 공액대칭(Conjugate and Conjugage Symmetry)

$$x^*(t) \leftrightarrow a^*_{-k}$$

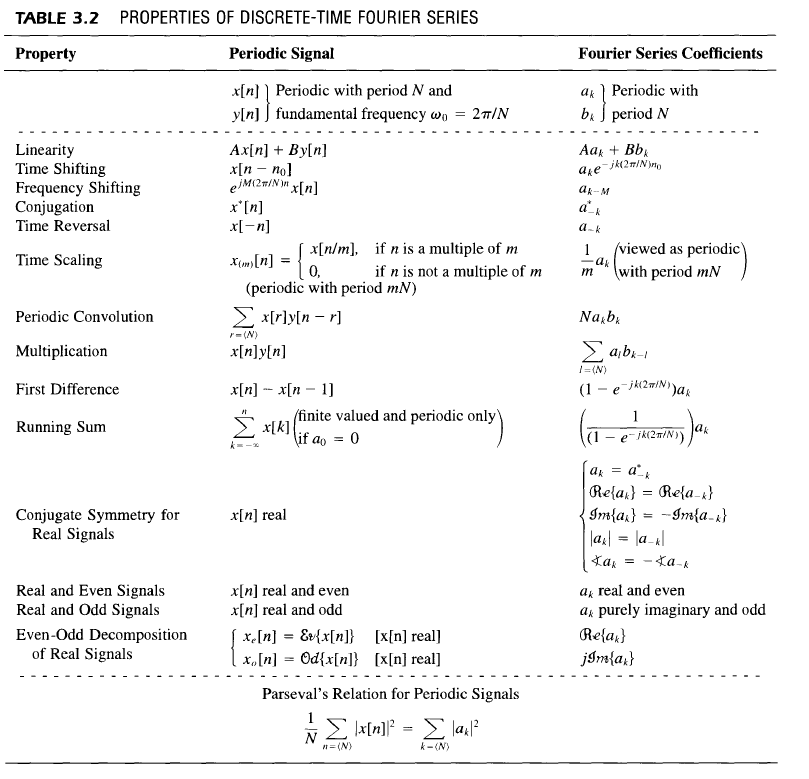
• x가 실수일 때는 앞서 확인한 것처럼 공액대칭(conjugate symmetric) 을 이룸

$$a_{-k}=a^*_k$$

• 아래 표를 참고하면 우함수/기함수 조건이 추가되었을 때의 계수의 관계를 더 확인할 수 있음

3.5.7 연속시간 주기신호에 대한 Parsival의 관계

$$\frac{1}{T}\int_T |x(t)|^2 dt=\sum_{k=-\infty}^{\infty}|a_k|^2$$

• 좌변은 주기신호 x(t)의 한 주기동안의 평균 전력, $

  a_k

  ^2$ 은 k번째 고조파 성분의 평균 전력임(아래 식을 통해 확인 가능)

$$\frac{1}{T}\int_T |a_ke^{jkw_0 t}|^2 dt=|a_k|^2$$

• 즉 위 법칙은 총 평균전력이 그 신호의 모든 고조파 성분들에서 평균전력의 합과 같다는 의미

3.5.8 연속시간 푸리에 급수의 특성 요약

3.6 이산시간 주기신호의 푸리에 급수 표현

• 이산시간 주기신호의 푸리에 급수 표현은 유한급수기 때문에 수렴에 관한 수학적인 문제는 없음

3.6.1 조화적으로 관련된 복소지수의 선형결합

• 주기적인 신호는 모든 n값과 기본 주기 N(최소 양의 정수)에 대해 다음과 같이 표현가능

$$x[n]=x[n+N]$$

• 주기적인 모든 이산시간 복소지수 신호는 다음과 같이 표현 가능

$$\Phi_k[n]=e^{jkw_0n}=e^{jk(2\pi /N)n}, \quad k=0, \pm 1, \pm 2, \cdots$$

• 연속시간과는 다르게 k값에 따라 같아 지는 애들이 발생함

$$\Phi_k[n]=\Phi_{k+rN}[n]$$

• 따라서 이산시간 푸리에 급수는 서로 다른 급수가 들어가는 구간만을 필요로 함(무한대의 항을 다 더할 필요가 없음)

3.6.2 주기신호의 푸리에 급수 표현의 결정

• 위의 내용을 통해 이산 신호는 기본 주기가 N일때 N개의 다른 복소지수의 합으로 표현가능하다는 것을 알게 됨
• 즉 계수식과 신호와의 관계를 표현하면 아래와 같고 이산시간 푸리에 급수쌍(pair)으로 불림

$$x[n]=\sum_{n=<N>}a_ke^{jkw_0n}$$ $$a_k=\frac{1}{N}\sum_{n=<N>}x[n]e^{-jkw_0n}$$

• 마찬가지로 위가 종합식 아래가 분석식이라고 불리며 $a_k$는 $x[n]$의 스펙트럼 계수라고 불림
• 항의 갯수가 증가하면서 수렴성을 보기 위해서 다음의 근사 식을 정의

$$\hat{x}[n]=\sum_{k=-M}^{M}a_ke^{jk(2\pi/N)n}$$

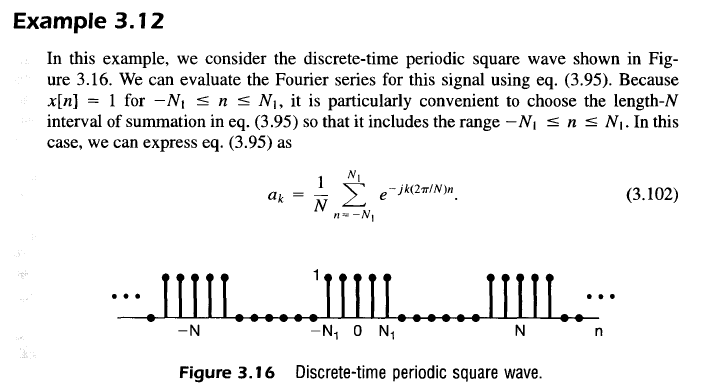
• 아래 그림은 $N=9, 2N_1+1=5$로 했을 때의 결과

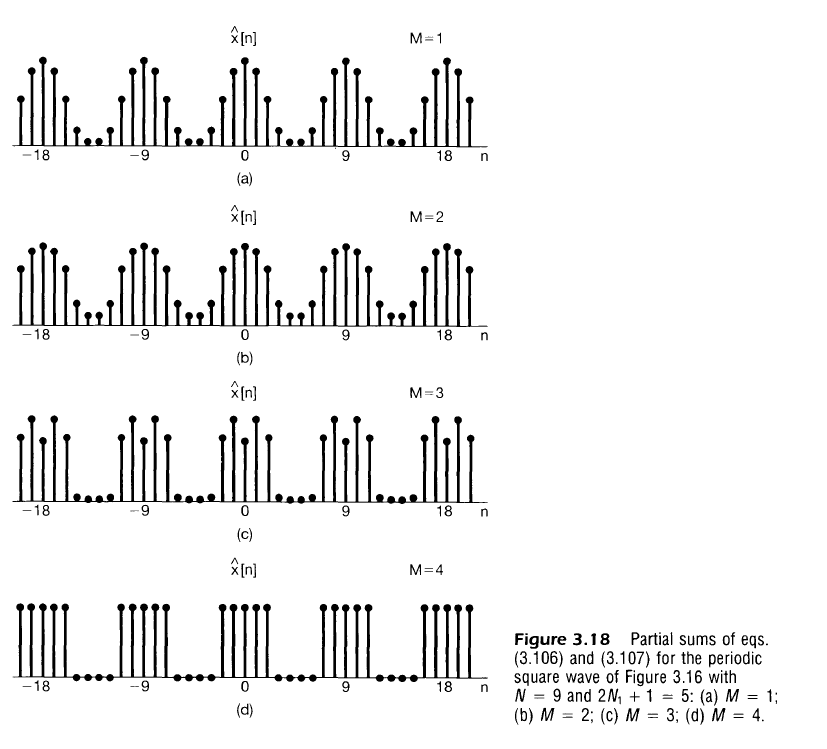
• M=4에 대해서 원래의 식과 정확히 일치하는 것을 확인 가능(해당 주기에서 모든 다른 급수 사용했을 때)
• 일반적으로 이산시간 푸리에 급수에는 수렴과 Gibbs 현상이 없음
• 이산시간 주기 수열을 유한한 수 N로 표현 가능하기 때문
• 정리하면 이산시간 주기 수열을 N의 수만큼 다른 복소함수의 합으로 표현했을 때 기존의 함수와 푸리에 급수는 같음
• 연속 시간은 연속 시간을 표현하기 위해 무한 개의 푸리에 급수가 필요하기 때문에 유한 부분합은 어느것도 정확한 x(t)값을 나타내지 못하며 수렴에 대한 문제가 발생할 수 있음

3.7 이산시간 푸리에 급수의 특성

• 연속시간과 많이 유사함
• 이 부분에서는 연속시간과 차이가 있는 몇몇 성징들에 한해서만 논의함
• 다음과 같이 기본 변환을 정의함

$$x[n]\leftrightarrow a_k$$ $$y[n]\leftrightarrow y_k$$

3.7.1 곱셈

$$x[n]y[n] \leftrightarrow d_k=\sum_{l=<N>}a_lb_{l-k}$$

• 더하는 변수가 N개 샘플의 구간으로 한정되는 것을 제외하면 동일
• 이를 주기적 컨볼루션 으로 표현함

3.7.2 일차 차분(First difference)

• 연속시간 푸리에 급수의 미분성질과 대응됨

$$x[n]-x[n-1]\leftrightarrow (1-e^{-jk(2\pi/N)}a_k$$

• 푸리에 급수 계수의 유도가 원래의 수열보다 일차 미분에 의한 것이 더 쉬울 때 사용됨

3.7.3 이산시간 주기신호의 Parseval의 관계

• 연속시간과 비슷하게 정의되고 의미도 같다
• 전체 형균전력은 각 k번째 고조파 성분의 평균전력의합과 동일

$$\frac{1}{N}\sum_{n=<N>}|x[n]|^2 = \sum_{k=<N>}|a_k|^2$$

3.8 푸리에 급수와 LTI 시스템

• 앞서 말했듯이 임펄스 응답$h(t),h[n]$에 대한 시스템 함수 $H(t),H[n]$은 다음과 같다

$$H(s)=\int_{-\infty}^{+\infty}h(\tau)e^{-s\tau}d\tau$$ $$H(z)=\sum_{k=-\infty}^{+\infty}h[k]z^{-k}$$

• 이 장과 다음 장의 연속시간 신호와 시스템에 대해서 $Re(s)$는 0인 경우만 고려하기 때문에 $s=jw$일때 시스템 함수는 주파수 응답을 의미하게 됨

$$H(jw)=\int_{-\infty}^{+\infty}h(\tau)e^{-jw\tau}d\tau$$

• 유사하게 이산신호와 시스템에서는 $

  z

  =1$인 시스템에 대해 고려하므로 $z=e^{jw}$로 제한됨 이떄 시스템 응답은 다음과 같이 정의됨

$$H(e^{jw})=\sum_{n=-\infty}^{+\infty}h[n]e^{-jwn}$$

• 연속시간에서 $e^{jwt}$ 또는 이산시간에서 $e^{jwn}$의 형태를 갖는 복소지수 신호에 대한 응답은 시스템의 주파수응답의 항으로 표현하는데 간단함

$$y(t)=\sum_{k=-\infty}^{+\infty}a_kH(jkw_0)e^{-jkw_0t}$$ $$y[n]=\sum_{k=<N>}a_kH(e^{-j2\pi k/N})e^{-jk(2\pi /N)n}$$

• 시스템함수가 잘 정의되어야지 위의 식들이 의미를 가질 수 있음
• 이는 고려중인 LTI 시스템이 안정상태인 경우를 뜻함

3.9 필터링

• 주파수 성분의 상대적인 크기를 변화시키거나 주파수 성분의 어떤 부분을 완전히 제거하는 과정
• 스팩트럼의 모양을 변화시키는 선형 시불변 시스템을 주파수 형성 필터(frequency-shaping filters)라 한다
• 원래 왜곡되지 않고, 다른 것들을 심하게 감쇄하거나 제거시키지 않는 어떤 주파수들을 통과시키도록 설계된 시스템을 주파수 선택 필터(frequency selected filters 라고 한다
• 필터링은 근사적으로 선택된 주파수 응답으로 LTI 시스템을 통해 쉽게 구할 수 있고 주파수 영역 기법은 이런 응용영역을 시험해 볼 수 있는 이상적인 수단을 제고앟ㅁ

3.9.1 주파수 형성 필터

• 오디오 시스템에 주로 쓰임
• 3.22 등가회로 정확하게 이해하지 못함
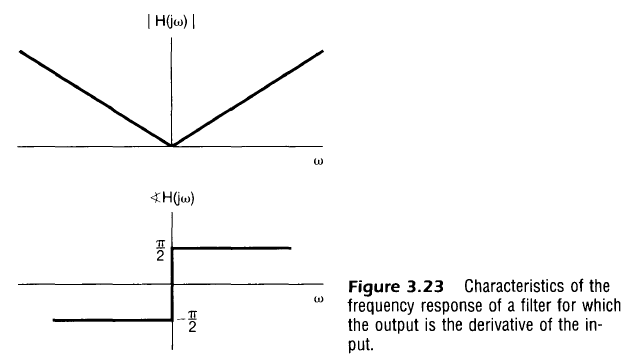
• 미분필터 : 주파수 응답이 $H(jw))=jw$, $w$값이 크루록 주파수 응답의 양이 더 커짐
  • 미분 신호에서 빠른 변화나 천이를 향상시키는데 유용
  • 화상 처리에서 경게를 선명하게 해주기도 함(문제 3.70)
• 이미지에서 경게의 수직방향에서는 신호가 급격히 변화여 경계의 주파수는 고주파로 집중되며, 수직방향에서 경계의 주파수는 저주파로 집중됨
• 화상의 경계에서 미분치는 밝기가 느리게 변화하는 영역보다 크기 때문에 필터의 효과는 경계에서 뚜렷하게 나타남
• 이산시간 LTI 필터 또한 7장에서 논의하겠지만 연속시간 신호를 처리하기 위해서, 디지털 프로세서를 이용하여 동작하는 이산시간 시스템의 이용을 포함함
  • 시간급수 정보의 분석은 보통 이산시간 필터의 사용을 수반함
• 간단한 이산시간 필터의 예로 평균치 필터를 들 수 있음

$$y[n]=\frac{1}{2}(x[n]+x[n-1])$$

• 이 때의 주파수 응답은 다음과 같음

$$H(e^{jw})=e^{-jw/2}cos(w/2)$$

• 이 필터는 $w=0$일 수록 더 큰 값을 가지며 $\pi$값으로 증가시키면 감소함, 고주파는 저주파에 비해 더 감쇄함

3.9.2 주파수 선택 필터

• 주파수의 한 대역을 정확히 또는 근사적으로 선택하거나 제거하는 필터의 한 종류
• 방송 시스템에 잘 사용됨(8장) : ex 진폭 변조(AM)
• 저역통과 필터 는 고주파를 감쇄시키거나 제거시키는 필터
• 고역통과 필터 어느 주파수의 대역은 토오가시키며 그보다 높거나 작은 주파수는 감쇄
• 차단주파수(cut-off frequency) 는 통과되는 주파수와 제거되는 주파수의 즉 토오가대역과 정지대역 사이의 경계로 정의됨
• 이상적 주파수 선택 필터(Ideal freqeuency-selective filter) 어떤 주파수에서 복소지수를 왜곡없이 완벼갛게 통과시키며 다른 주파수에서 신호를 완벽하게 제거시키는 필터
• 아래는 그중 하나인 이상적 저역통과 필터, 이상적 고역통과 필터, 이상적 대역필터이다
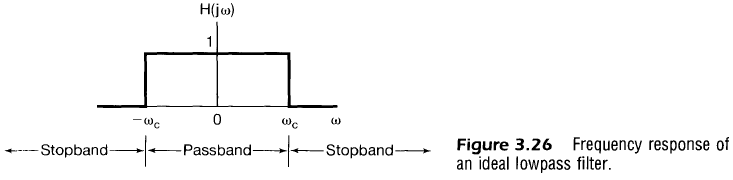
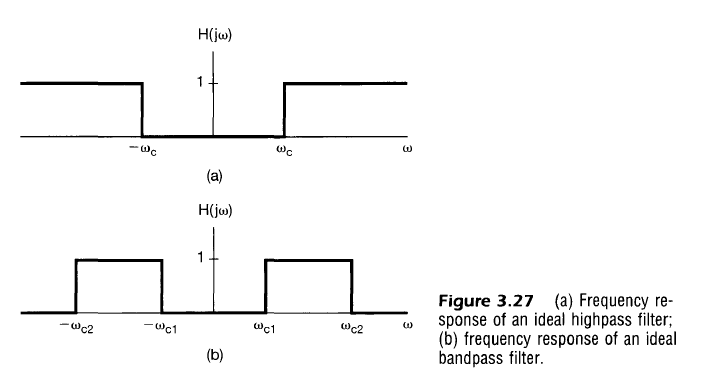
• 각각의 필터는 $w=0$에 대칭, 이는 정현파 신호보다 복소지수 신호$e^{jwt}$를 사용하는 이유기도 함
• 이산시간도 마찬가지로 표현 가능, 단 이산신호 필터는 $\2pi$의 주기성 가짐
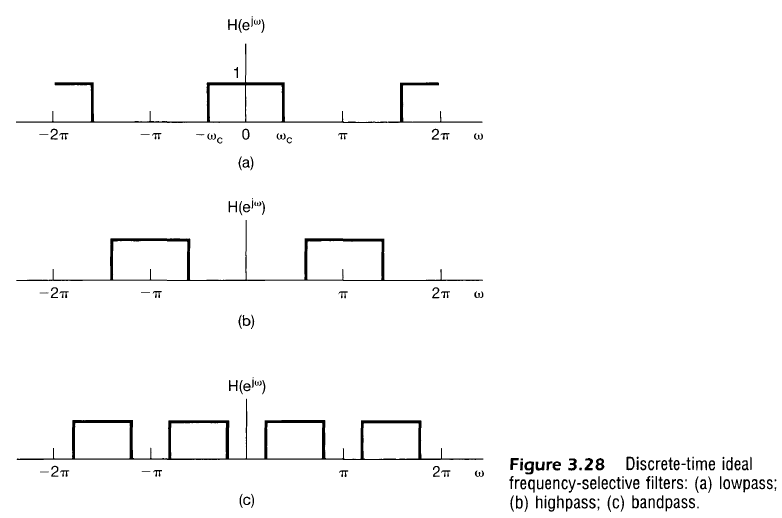
• 이상적 필터는 다양한 응용 분야에 이상화된 시스템 구성을 설명하는데 유리하나 실제로 실현불가능하고 근사화됨
• 또한 실현하더라도 몇몇 이상적 필터의 특성은 특정 응용분야에 대해서 설명할 수 없을 수도 있으며, 비이상적 필터가 실제로 더 바람직할 수 있음

3.10 미분방정식으로 표현되는 연속시간 필터의 예

• 필터링은 미분방정식으로 표현되는 LTI 시스템의 이용으로 구현됨
  • 이유 1. 필터링 동작으로 이루어짐을 예측할 수 있는 많은 물리적 시스템은 미분 또는 방정식으로 이루어짐
  • 이유 2. 아날로그나 디지털하드웨어를 이용하여 구현하기 용이함
  • 이유 3. 미분방정식으로 표현되는 시스템은 이상적이거나 다른 바람직한 특성들을 갖는 필터를 설계하는데 범위가 폭넓고 유연함

3.10.1 간단한 RC 저역통과 필터

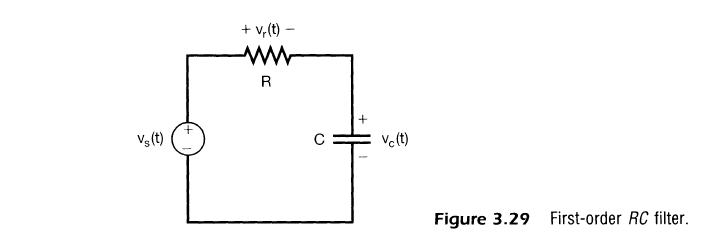
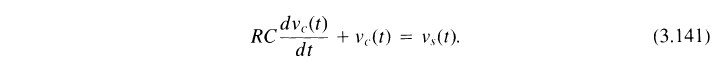
• 주파수 응답 $H(jw)$를 구하면 다음과 같음

$$H(jw)=\frac{1}{1+RCjw}$$

• 비이상적인 저역통과 필터라고 볼 수 있음
• 단위 임펄스 응답, 계단응답(Unit impulse response, Unit step response)와 비교
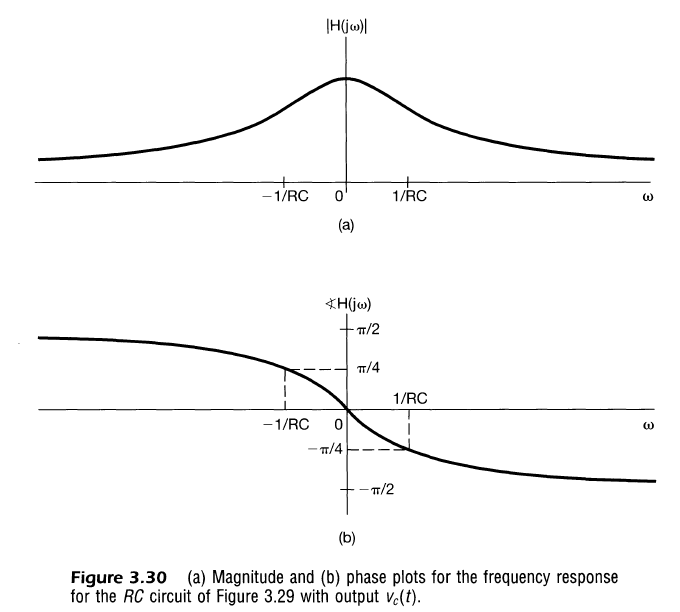
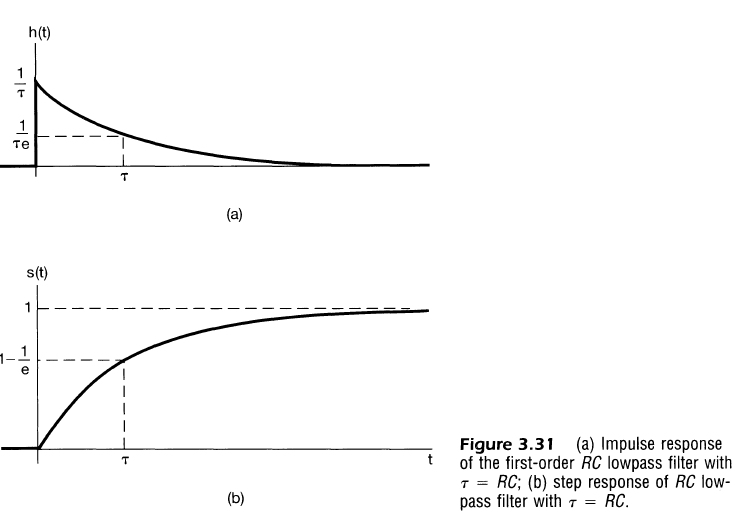
• RC값의 증가가 주파수 응답에 영향을 줌
• 위의 그림을 통한 예제를 볼 수 있듯이 필터의 주파수 응답과 응답시간 간의 Tradeoff 존재

3.10.2 간단한 RC 고역통과 필터

• 주파수 응답을 다음과 같이 정의하자

$$H(jw)=\frac{jwRC}{1+RCjw}$$

• 비이상적 고역파 필터
• 단위 임펄스 응답, 계단응답(Unit impulse response, Unit step response)와 비교
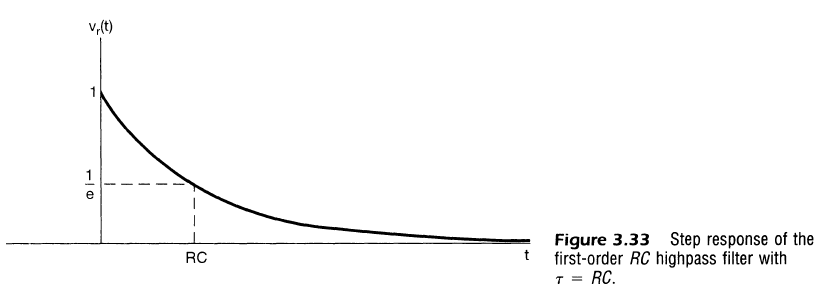
• RC값의 증가가 주파수 응답에 영향을 줌
• 전기적 기계적 필터들의 예제를 통해 통과대역에서 정지대역으로 급격한 변환이 없으며, 응답 동작을 제어하는 단지 하나의 매개변구(전기적인 경우 RC)를 가지고 있는 것을 확인 가능
• 더 복잡한 고차원 미분방정식에 의해 표현되는 필터를 통해서 시간 응답과 주파수 응답 간의 trade–off를 더욱더 제어할 수 있으며, 그런 필터는 특성이 폭넓다

3.11 차분방정식에 의해 표시되는 이산시간 필터의 예

• 실제로 특별 또는 일반적인 목적의 디지털 시스템에서 효율적으로 동작되기 때문에 중요
• 무한 길이의 임펄스 응답(IIR 시스템)을 가지고 있거나, 유한 길이의 임펄스 응답(FIR 시스템)을 가지고 있음
• 전자는 연속시간 시스템에 직접적으로 대응되는 반면 후자는 디지털 시스템에서 중요하게 고려됨

  3.11.1 1차 회귀성 이산시간 필터

• 아래 1차 차분방정식에 대한 필터

$$y[n]-ay[n-1]=x[n]$$ $$H(e^{jw})=\frac{1}{1-ae^{-jw}}$$ $$h[n]=a^nu[n]$$ $$s[n]=\frac{1-a^[n+1]}{1-a}u[n]$$

• a	의 값이 작을수록 응답을 빨리함

• a	$\geq 1$ 이면 불안정, 유한한 응답을 가질 수 없음

• 앞서 말했듯이 푸리에 기본 기법과 주파수 영역분석은 복소지수에 대한 유한한 응답을 가지는 시스템에 중점을 둠

3.11.2 비회귀성 이산시간 필터

• FIR 비회귀성 차분방정식의 일반적인 형태는 다음과 같음

$$y[n]=\sum_{k=-N}{M}b_kx[[n-k]$$

• 가중평균(weighted average) 이라고 불림
• 예시가 이동평균(Moving average)

$$H(e^{jw})=\frac{1}{N+M+1}\sum_{k=-N}^M e^{-jwk}=\frac{1}{N+M+1}e^{-jw(N-M)/2}\frac{sin(w(M+N++1)/2)}{sin(w/2)}$$

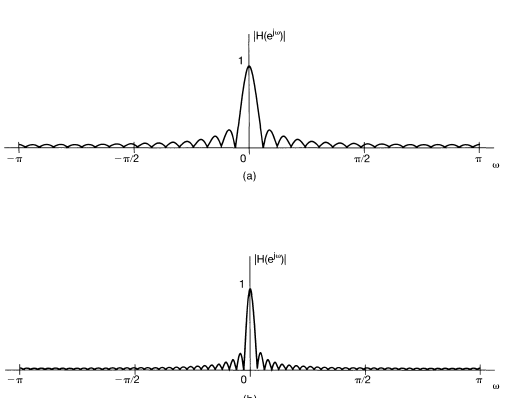
• 모든 FIR 시스템의 임펄스 응답이 유한길이에서 $b_k$값이 나오므로 어떠한 b를 선택해도 합이 가능 $\rightarrow$안정함
• 실시간 처리에서 인과관계는 필수이므로 $N\leq 0$이어야 하나 기록된 신호 처리시에는 $N>0$사용 가능

3.12 요약

• 푸리의 급수의 가장 중요한 성질 중 하나는 복소지수의 고유함수 특성의 직접적인 결과라는 것
• 주파수 함수는 LTI 시스템의 특성을 가지며 시스템의 주파수 응답
• 주파수 응답의 검토로 필터링과 연결 가능