신호 및 시스템 Chapt 2

Alan V. Oppenheim, Signals and Systems 책 내용입니다.

2. 선형 시불변 시스템

• 많은 물리적인 과정들이 선형성, 시불변성을 가지고 있어 LTI 시스템으로 모델링 가능
• LTI 시스템은 상당히 자세히 분석할 수 있음(중첩 특징으 가짐)
• 단위 임펄스로 이산시간과 선형 시간에서 매우 일반적인 신호들을 표현 가능
• 즉 단위 임펄스에 대한 응답의 항으로 LTI 시스템의 완벽한 특성을 알 수 있음

2.1 이산시간 LTI 시스템: 컨볼루션 합(Convolution Sum)

2.1.1 임펄스 항을 이용한 이산신호의 표현

$x[\alpha]\delta[n+\alpha]$

• 전체 신호를 위의 신호로 분할 가능
• 이동 특성 : 즉 간단한 형식으로 나타내면 신호는 다음과 같이 표현 가능함 $x[n]=\sum_{k=-\infty}^{+\infty}x[k]\delta[n-k]$

2.1.2 이산시간 단위 임펄스 응답과 LTI 시스템의 컨볼루션 합

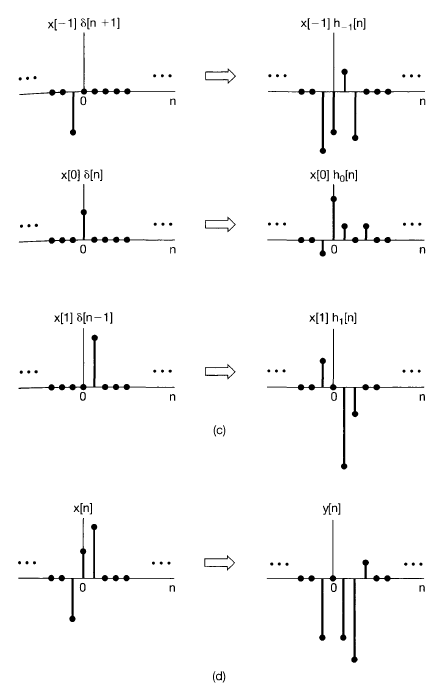
• $h_k[n]$을 이동된 단위 임펄스 $\delta[n-k]$에 대한 선형 시스템의 응답이라 할때 중첩 특성에 의해서 시스템의 응답 $y[n]$은 다음과 같다 $y[n]=\sum_{k=-\infty}^{+\infty}x[k]h_k[n]$
• $h_k[n]$는 $h_0[n]$을 k만큼 shift한 것과 같으므로 단위 임펄스 응답을 다음과 같이 정의 $h[n]=h_0[n]$
• 따라서 시스템 응답을 다시한번 정리하면 $y[n]=\sum_{k=-\infty}^{+\infty}x[k]h[n-k]$
• 이를 컨볼루션 합 또는 중첩 합으로 정의되고 다음과 같이 표현한다 $y[n]=x[n]*h[n]$
• 위 식은 입력 x[k]에 대한 응답이 h[n-k] 즉 h[n]의 이동 및 시간 배율된 것(echo)된 것와 비슷함
• 실제의 출력은 모든 응답의 중첩
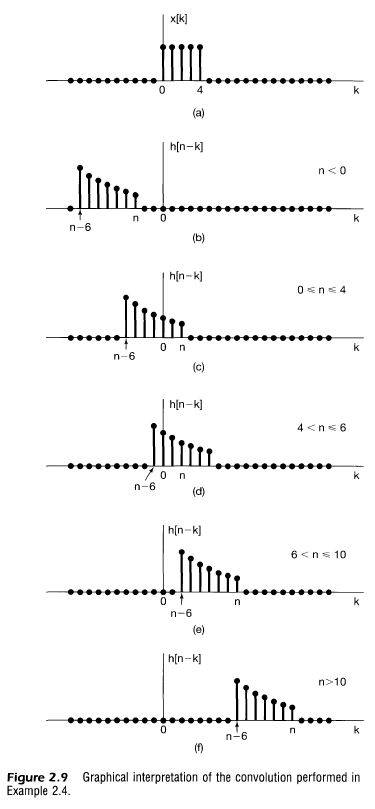
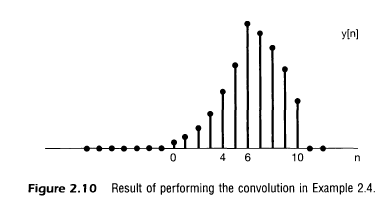
• 컨벌루션 합을 이용하여 $y[n]$을 계산하기 위한 유용한 방법
  • 두 신호 $x[k]$와 $h[n-k]$를 k의 함수로 보면서 시작
  • $h[n-k]$는 $h[k]$응답을 반전하고 n만큼 shift한 것
  • 즉 함수 $g[k]$=$x[k]h[n-k]$를 얻기
  • $g[k]$의 순차열에서 모든 샘플을 더한것이 바로 시간 n에서의 출력
• 컨볼루션의 계산은 순차열 $h[n-k]$가 $x[k]$를 지나가는 것으로 묘사되기도 함

2.2 연속시간 LTI 시스템: 컨볼루션 적분(Convolution Integral)

• 1.4.2절의 논의 내용과 같이 지속시간이 너무 짧아서 실제적이고 물리적인 시스템에서 무시될 수 있는 이상화된 펄스로 생각
• 임의의 연속시간 신호는 이상화되어 기간이 짧은 펄스나 등가적으로 임펄스를 통해 표현할 수 있음

2.2.1 임펄스를 이용한 연속시간 신호의 표현

• 신호를 다음과 같이 근사하게 되면 모든 신호는 지연된 펄스들의 선형결합으로 표현 가능 $\delta_\Delta(t)=\begin{cases} 0, \quad 0\leq n<\Delta \\ \frac{1}{\Delta}, \quad else \end{cases}$
• 다시 정리하면 다음과 같은 표현을 얻을 수 있음 $\hat{x}(t)=\sum_{k=-\infty}^{+\infty}x(k\Delta)\delta_\Delta[t-k\Delta]\Delta$

• $\Delta$가 0으로 접근하기 때문에 근사함수는 단위 임펄스 함수와 가까워지고 위 식은 다음과 같이 정리 가능 $x(t)=\int_{-\infty}^{+\infty}x(\tau)\delta(t-\tau)d\tau$

• 위 식을 이산시간과 동일하게 임펄스의 선별특성(sifting property) 이라고 말할 수 있다

2.2.2 연속시간 단위 임펄스 응답과 LTI 시스템의 컨볼루션 적분 표현

• 근사함수를 사용해서 다음과 같이 정의 가능 $\hat{y}(t)=\sum_{k=-\infty}^{+\infty}x(k\Delta)h_\Delta[t-k\Delta]\Delta$
• 극한을 취하면 출력은 다음과 같이 표현 가능(마찬가지로 $h(t)=h_0(t)$로 정의) $y(t)=\int_{-\infty}^{+\infty}x(\tau)h(t-\tau)d\tau$
• 이는 컨볼루션 적분(Convolution Integral) 또는 중첩 적분으로 불리고 아래와 같이 표현됨 $y(t)=x(t)*h(t)$
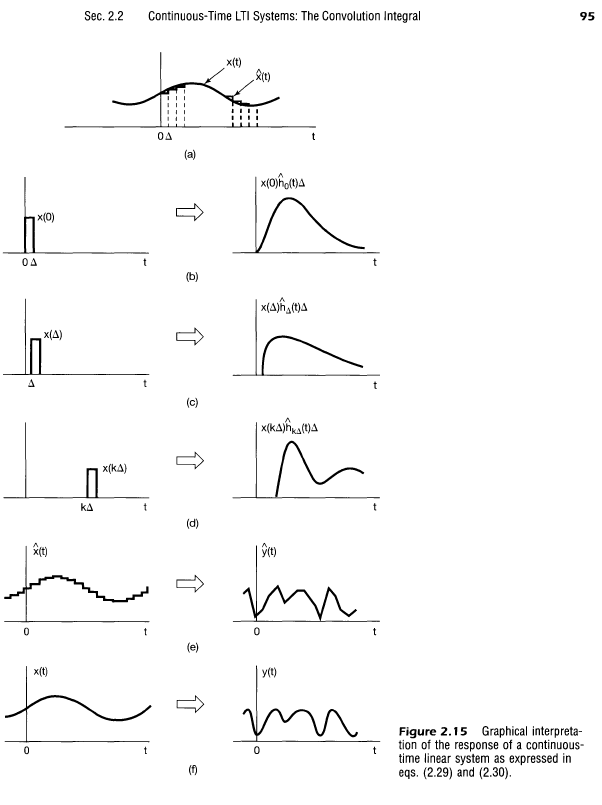
• 이산 신호와 동일하게 $h(t-\tau)$를 shift한걸로 계산해도 됨

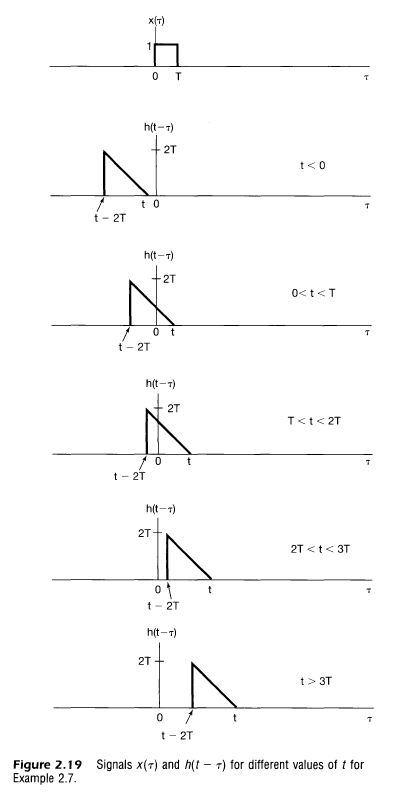
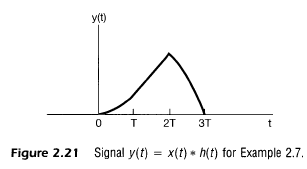
2.3 선형 시불변 시스템의 특성

• 앞의 두 장을 정리하면, 단위 임펄스 응답을 통해 연속시간 및 이산시간 LTI 시스템의 특성을 확인할 수 있다 $y[n]=\sum_{k=-\infty}^{\infty}x[k]h[n-k]=x[n]*h[n]$ $y(t)=\int_{-\infty}^{+\infty}x(\tau)h(t-\tau)d\tau=x(t)*h(t)$
• 이러한 특성들은 LTI 시스템에서만 유효함
• 비선형 시슽메의 단위 임펄스 응답은 시스템의 행동을 완전히 특정짓지는 못함

2.3.1 교환법칙

• 선형 시불변 시스템에서는 교환법칙이 성립함 $y[n]=x[n]*h[n]=h[n]*x[n]=\sum_{k=-\infty}^{\infty}h[k]x[n-k]$
• 이는 n’=n-k으로 정의한 뒤에 정리하면 증명됨
• 연속신호도 마찬가지로 증명가능. 의미하는 바도 동일

2.3.2 분배법칙

$x[n]*(h_1[n]+h_2[n])=x[n]*h_1[n]+x[n]*h_2[n]$ $x(t)*(h_1(t)+h_2(t))=x(t)*h_1(t)+x(t)*h_2(t)$

• 분배법칙은 시스템 상호교환에 대한 유용한 표현
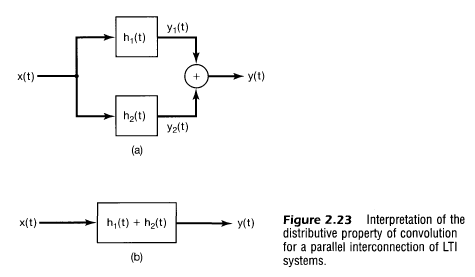
• 교환법칙과 같이 적용해서 전체 시스템응답으 개별 시스템응답의 합과 동일 $(x_1[n]+x_2[n])*h_2[n]=x_1[n]*h[n]+x_2[n]*h[n]$ $(x_1(t)+x_2(t))*h_2(t)=x_1(t)*h(t)+x_2(t)*h(t)$

2.3.3 결합법칙

$x[n]*(h_1[n]*h_2[n])=(x[n]*h_1[n])*h_2[n]$

• 적분과 합들을 이용하면 쉽게 증명 가능(연습문제 2.43)
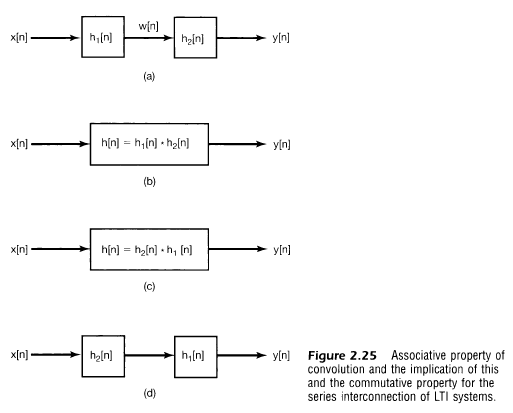
• 교환법칙에 의해 직렬 시스템의 순서는 서로 상관이 없음
• 비선형 시스템에서는 성립하지 않음

2.3.4 메모리가 있는 LTI 시스템과 없는 LTI 시스템

• 메모리 없는 시스템은 $n\neq 0$일때 $h[n]=0$이므로 다음과 같은 성질을 가짐 $h[n]=K\delta[n]$
• 따라서 시스템 응답도 다음과 같음 $y[n]=Kx[n]$

2.3.5 LTI 시스템의 가역성

• 출력 신호를 원래의 입력 신호로 재변환 시키는 역시스템(inverse system)이 존재할때 이를 가역적이라고 한다
• LTI 시스템이 가역적이면 이러한 시스템은 LTI 역특성을 가짐 (문제 2.50)
• 따라서 $h_1(t)$가 $h(t)$의 역시스템이 되려면 다음의 식이 성립해야 한다 $h(t)*h_1(t)=\delta(t)$ $h[n]*h_1[n]=\delta[n]$

2.3.6 LTI 시스템에 대한 인과성

• LTI 시스템에서는 인과성이 성립하려면 $k>n$에 대해서 $h[n-k]=0$이 성립해야 되므로 다음의 조건이 성립해야 됨 $h[n]=0, n<0$
• 따라서 시스템 응답은 다음의 식으로 변형 가능 $y[n]=\sum_{k=-\infty}^{n}x[k]h[n-k]$
• 이산시간도 마찬가지로 $h(t)=0 , t<0$

• 따라서 시스템 응답은 다음의 식으로 정리 가능 $y(t)=\int_{-\infty}^t x(\tau)h(t-\tau)d\tau$

• 인과성이 시스템의 특성이기는 하지만 일반적으로 신호가 n<0또는 t<0에 대해 0이면 인과적이라고 함

2.3.7 LTI 시스템에 대한 안정성

• 앞서 배운 것처럼 시스템이 “안정하다(stable)” 는 말은 제한된 입력을 줬을때 제한된 출력을 야기한다는 것을 의미
• LTI 시스템에서 식으로 정리하면 다음과 같다

$$|x[n]|<B,for \ all \ n$$

• 컨볼루션 합을 정리 후 각 집합에 성질에 따라 다음과 같이 유도 가능 $|y[n]|\leq \sum_{k=-\infty}^{\infty}|h[k]||x[n-k]|=B\sum_{k=-\infty}^{\infty}|h[k]|$
• 즉 위의 식을 통해 임펄스 응답 이 무한대보다 작다면 y[n]은 크기가 제한되어 시스템이 안정하다고 결론낼 수 있다
• 따라서 아래의 식은 LTI 시스템의 안정성을 보장해 주기 위한 충분조건 $\sum_{k=-\infty}^{+\infty}|h[k]|<\infty$
• 연속시간도 마찬가지로, 임펄스 응답이 완전하게 적분 가능하다면, 즉 아래의 식이 성립하다면 시스템은 안정함 $\int_{-\infty}^{\infty}|h(\tau)|d\tau<\infty$

2.3.8 LTI 시스템의 단위 계산 응답(Step response)

• LTI 시스템의 동작을 설명하기 위해 계단응답으로 가끔씩 표현하는 것이 유용할 때가 많음 $s[n]=u[n]*h[n]$
• 식으로 정리하면 다음과 같은 의미를 가짐 $s[n]=\sum_{k=-\infty}^{n}h[k]$
• 관계식을 나타내면 다음과 같음 $h[n]=s[n]-s[n-1]$
• 연속시간도 마찬가지임 $s(t)=\int_{-\infty}^{t}h(\tau)d\tau$
• 즉 아래의 성질을 가짐 $h(t)=\frac{ds(t)}{dt}=s'(t)$
• 따라서 이산시간 및 연속시간 모두에서 단위 계단응답도 그로부터 단위 임펄스 응답을 유추해 낼 수 있기 때문에 LTI 시스템을 표현하는데 사용될 수 있다(문제 2.45번을 참고)

2.4 미분방정식과 차분방정식으로 표현된 인과적 LTI 시스템

• 연속시간 시스템의 각 class에서 입력과 출력이 선형 상게수 미분방정식(Linear constant-coefficient differential equation) 로 표현됨
• 이산시간 시스템에서는 입력과 출력이 선형 상계수 차분방성식(Linear constant-coefficient difference equation) 의 관계에 있음

2.4.1 선형 상계수 미분방정식

• 예로 간단한 일차 미분방정식을 들면 $\frac{dy(t)}{dt}+2y(t)=x(t)$
• 이러한 방정식이 중요한 이유는 입력과 출력의 관계를 표현해 주기 때문임
• 정확한 해를 얻기 위해서는 미분방정식의 정보 + 부가정보가 필요함
• 부가 정보에 따라서 시스템의 응답이 다른 관꼐가 나올 수 있음 (초기조건 같음)
• 에제(2.14)에 일차 상미분방정식을 푸는 일반적인 방법인 특수해(particular solution) $y_p(t)$ 와 고유해(homogeneous solution) $y_h(t)$ 의 설명이 있음 $y(t)=y_p(t)+y_h(t)$
• 이를 통해서 미분방정식의 응답은 특수해와 고유해의 합으로 이루어지고 고유해는 시스템의 정상응답(stationary response)라고도 불림(문제 2.61, 2.62에서 다뤄짐)
• 사용되는 부가조건은 일반적으로 시스템의 초기휴지조건임
  • 즉 입력이 0일때까지는(입력이 들어오기 전까지는) 출력도 0으로 맞춰주는 것이 일반적
• 일반적으로 N차 선형계수 미분방정식은 다음과 같이 주어짐 $\sum_{k=0}^N a_k\frac{d^k y(t)}{dt^k}=\sum_{k=0}^M b_k \frac{d^k x(t)}{dt^k}$
• N=0을 만족하면 식을 다음과 같이 정리 가능하며, 이때는 어떠한 초기조건도 필요하지 않음 $y(t)=\frac{1}{a_0}\sum_{k=0}^M b_k \frac{d^k x(t)}{dt^k}$
• y(t)는 두 부분으로 구성된다고 할 수 있는데 위의 식의 특수해와 다음 다차 미분방정식을 만족시키는 해의 합. 이를 만족시키는 해를 자연 응답(Natural Response) 라고 부름 $\sum_{k=0}^N a_k\frac{d^ky(t)}{dt^k}=0$
• 이 책에서는 모두 초기휴지 조건을 사용할 것($t\leq t_0$에서 $x(t)=0$이면 $t\leq t_0$에서 $y(t)=0$으로 가정
  • 즉 초기조건을 정리하면 다음과 같음 $y(t_0)=\frac{dy(t_0)}{dt}=\cdots=\frac{d^{N-1}y(t_0)}{dt^{N-1}}=0$
• 초기휴지상태의 조건하에서 위에 묘사된 시스템은 인과적이고 LTI이다

2.4.2 선형 상계수 차분방정식

• 이산 시간에 대해서는 다음과 같이 차분방정식으로 표현 가능 $\sum_{k=0}^N a_ky[n-k]=\sum_{k=0}^M b_k x[n-k]$

• y[n]은 특수해와 아래의 다차방정식의 해의 합(자연 응답) 으로 구할 수 있음 $\sum_{k=0}^N a_ky[n-k]=0$

  • 마찬기지로 보조조건이 필요함
  • 위의 식이 성립하면 연속시간과 마찬가지로 인과적이며 LTI이다
• 이산시간의 경우 다른 방법을 제시하기도 하는데 위의 식을 다음과 같이 표현할 수 있다는 것부터 시작됨 $y[n]=\frac{1}{a_0}(\ \sum_{k=0}^M b_k x[n-k]-\sum_{k=1}^N a_ky[n-k] )$
• 위의 방정식은 이전 신호들에 의해 현재의 출력이 결정되는 반복 회귀적인 과정을 구체적으로 정리한 회귀 방정식(recursive equation) 이라 불린다.
• N=0이면 아래와 같이 식이 정리되고 비회귀방정식 이라 불린다. 이때는 현재의 출력값을 구하기 위해서 이전에 계산된 출력값을 반복회귀적으로 사용할 수 없다 $y[n]=\sum_{k=0}^M (\frac{b_k}{a_0})x[n-k]$
• 이 때는 연속시간에서와 마찬가지로 초기조건이 필요하지 않음
• 이러한 시스템의 임펄스 응답은 유한적으로만 값을 가짐 $h(t)=\begin{cases} \frac{b_0}{a_0}, \quad 0\leq n\leq M \\0, \quad else \end{cases}$
• 따라서 위와 같은 식에 의해서 구현된 시스템은 종종 유한 임펄스 응답(FIR) 시스템 이라고 불린다
• 반대로 $N\geq 1$일때, 즉 회귀적일때 보조조건들이 요구되며, LTI 시스템의 경우 이에 대응되는 LTI 시스템의 경우는 대게 무한구간의 임펄스 응답을 가지고 있끼 때문에 무한 임펄스 응답(IIR) 시스템 이라고 불러진다

2.4.3 미분방정식과 차분방정식으로 표현된 일차시스템의 블록선도 표현

• 선형 시불변 차분방정식, 미분방정식으로 표현된 시스템은 블록선도로 간단하고 자연스럽게 표현 가능
• 연습문제 2.57~2.60에 소개된 인과적 일차 시스템을 통해 블럭선도 표현의 기본 아이디어를 설명함
• 피드백 존재는 순환 성질의 직접적 결과임 $y[[n]=-ay[n-1]+bx[n]$
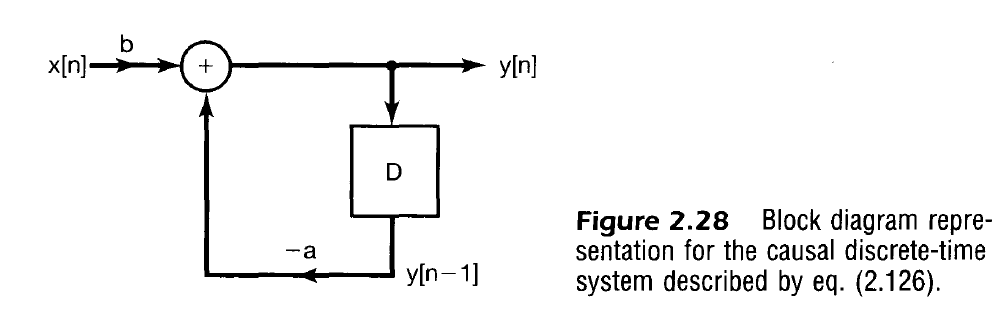
  • 이러한 시스템은 메모리가 있는 시스템이며 메모리로 이전 시간의 응답을 포함해야 함

• 연속 시스템도 마찬가지 $y(t))=\frac{1}{a}\frac{dy(t)}{dt}+\frac{b}{a}x(t)$

  

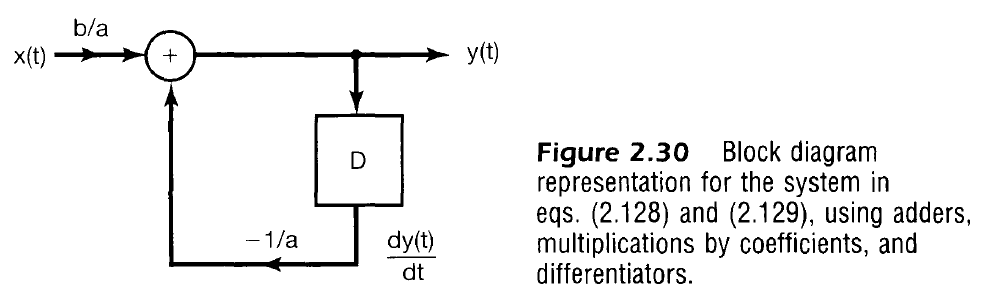
• 그러나 미분기는 구성하기 어렵고 에러나 잡음에 대단히 민감하기 때문에 실제적인 구성으로 이끄는 표현은 아님
• 더 널리 쓰이는 표현은 다음과 같이 다시쓰고 적분함으로써 얻을 수 있음 $y(t)=\int_{-\infty}^{t}\frac{dy(t)}{dt}dt=\int_{-\infty}^{t}[bx(t)-ay(t)]dt$
  • 시스템이 초기적으로 0이라고 가정했기 때문에 $y_{-\infty}=0$ 가능한 것
• 적분기는 opamp를 통해 구현할 수 있음(아날로그 컴퓨터와 현재의 아날로그 계산 시스템의 기본)

• 시스템 메모리의 저장 요소가 적분기라는 것에 유의 $y(t)=y(t_0)+\int_{t_0}^t [bx(\tau)-ay(\tau)]d\tau$

• 고차 시스템도 블록선도로 표현 가능 (연습문제 2.58,2.60 참고)

2.5 특이함수(Singularity functions)

2.5.1 이상화된 짧은 펄스로서의 단위 임펄스

• 단위 임펄스는 항등시스템의 임펄스 반응이라 어떤 신호$x(t)$에 대해서 다음이 성립함

$$x(t)=x(t)*\delta(t)$$

• 따라서 단위 임펄스는 다음과 같은 기본적 성질을 가짐, 단위 임펄스의 해석에 중요한 암시를 줌

$$\delta(t)=\delta(t)*\delta(t)$$

• 1.34절에서 배운 임펄스 근사함수를 사용하면 사실 매우 다르게 보이는 수 많은 신호들이 극한에서는 단위 임펄스처럼 행동하는 것을 확인할 수 있음
• 즉 $\delta$가 충분히 작다면 모든 신호에 대해 LTI 시스템의 응답이 본질적으로 같음

$$r_\Delta(t)=\delta_\Delta(t)*\delta_{\Delta}(t)$$

• 예제 2.16을 보면 극한값으로 갈수록 근사값과 신호가 같아지는 것을 확인할 수 있음

2.5.2 컨볼루션을 통한 단위 임펄스의 정의

• 단위 임펄스에 있어서 제일 중요한 것은 컨볼루션에 있음
• 선형 시스템 분석에서 신호가 선형시스템에 적용될 때 그 신호로써 단위 임펄스를 다음과 같이 다르게 정의함

$$x(t)=x(t)*\delta(t)$$

• 우리가 필요로 하는 단위임펄스 신호의 모든 특성은 연산정의(operational definition) 으로부터 얻어질 수 있음
• 모든 $t$에 대해 $x(t)=1$로 가정하면 단위 임펄스는 단위면적을 갖는 성질을 유도 가능

$$1=x(t)=x(t)*\delta(t)=\int_{-\infty}^{\infty}\delta(\tau))x(t-\tau)d\tau=\int_{-\infty}^{\infty}\delta(\tau)d\tau$$

• 함수 g(t)를 정의하면 t=0에 대해 다음의 식이 성립

$$g(0)=\int_{-\infty}^{\infty}g(\tau)\delta(\tau)d\tau$$

• 위의 식을 통해 다른 특성들을 결정하는데 유용
• 즉 아래의 두 식이 모두 성립함

$\int_{-\infty}^{\infty}g(\tau)f(\tau)\delta(\tau)d\tau=g(0)f(0)$ $\int_{-\infty}^{\infty}g(\tau)f(0)\delta(\tau)d\tau=g(0)f(0)$

• 위의 식은 신호를 $f(t)\delta(t)$로 정의한 것, 아래는 $f(0)\delta(t)$로 정의
• 즉 $f(t)\delta(t)$와 $f(0)\delta(t)$가 어떤 신호와 곱해지고 적분된다면 독립적으로 행동한다는 것을 확인할 수 있음
• 따라서 1.4.2절에서 유도된 특성과 동일

$$f(t)\delta(t)=f(0)\delta(t)$$

2.5.3 단위 이중항(doublet)과 다른 특이함수들

• 단위 임펄스는 특이함수중 하나이며, 이것들 각각은 컨볼루션 하에서의 행동에 따라서 기능적으로 정의됨
• 아래의 출력이 미분인 LTI 시스템에서 시스템의 단위 임펄스 응답은 단위 이중항 u_1(t) 라고 불리는 단위 임펄스의 미분임. 즉 다음과 같음

$y(t)=\frac{dx(t)}{dt}$ $\frac{dx(t)}{dt}=x(t)*u_1(t)$

• 유사하게 두번 미분인 $u_2(t)$를 LTI 시스템의 임펄스 응답으로 정의 가능, 다음과 같이 정리 가능

$$\frac{d^2x(t)}{dt^2}=\frac{d}{dt}\frac{dx(t)}{dt}=x(t)*u_2(t)=x(t)*u_1(t)*u_1(t)$$

• 즉 단위 이중항은 다음과 같이 정리 가능

$$u_k(t)=u_1(t)*\cdots*u_1(t), \quad k번 \ convolution$$

• 컨벌루션 성질에 의해서 넓이는 0임(x(t)=1로 가정하면 쉽게 구할 수 있음)

$$0=\frac{dx(t)}{dt}=x(t)*u_1(t)=\int_{-\infty}^{+\infty}u_1(\tau)d\tau$$

• $g(-t)을 컨볼루션해서 다음의 성질도 구할 수있음

$$\int_{-\infty}^{+\infty}g(\tau-t)u_1(\tau)d\tau=g(-t)*u_1(t))=-\frac{g(-t)}{dt}=-g'(-t)$$

• 유사한 방법으로 더 높은 차수의 특이함수에 대한 성질도 유도 가능(연습문제 2.69)
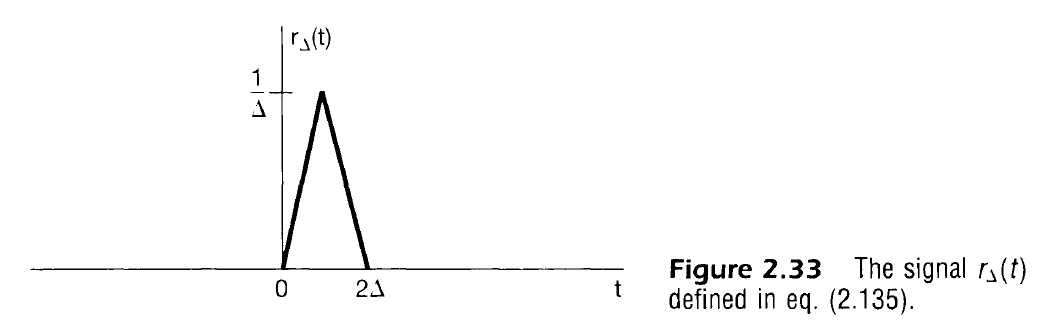
• 연습문제 2.72를 통해서 근사함수는 다음과 같이 표현 가능

$$\frac{d\delta_\Delta(t)}{dt}=\frac{1}{\Delta}[\delta(t)-\delta(t-\Delta)]$$

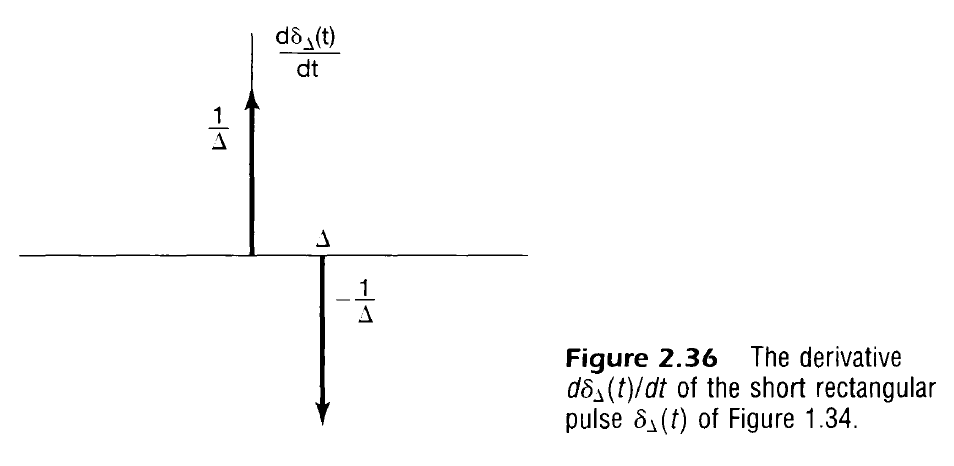
• 단위 임펄스의 차수가 다른 미분을 가지는 특이함수에 대해서 정의한 것처럼 단위 임펄스 함수의 적분으로 나타내는 신호들도 정의 가능
  • 단위 계단함수(Unit Step function)은 적분기의 임펄스 응답이기 때문에 다음과 같이 기능적으로 정의 가능

$$x(t)*u(t)=\int_{-\infty}{t}x(\tau))d\tau$$

• 즉 여러개의 적분기로 이루어진 시스템의 임펄스 응답은 다음과 같이 단순 컨볼루션으로 나타낼 수 있음

$$u_{-2}=u(t)*u(t)=\int_{-\infty}^{t}u(\tau)d\tau$$

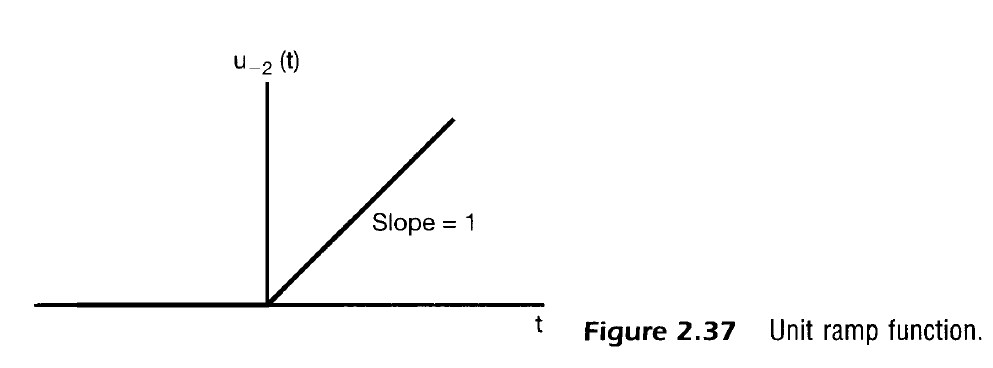
• 이는 단위 램프 함수(Unit ramp function) 이라 불리며, $u(t)$가 t<0일때 0이고, t>0 일때 1이므로 다음과 같이 정리 가능

$$u_{-k}=\frac{t^{k-1}}{(k-1)!}u(t)$$

• 따라서 단위 임펄스의 미분과는 다르게 적분은 컨볼루션 안에서 행동하는 이상 t가 각각의 값에 대해 정의될 수 있는 함수
• 이 때 $\delta(t))$와 $u(t)$는 다음과 같은 표현을 사용하는 것이 유용함

$\delta(t)=u_0(t)$ $u(t)=u_{-1}(t)$

• 미분기는 적분기의 역시스템이기 때문에 정수 k,r에 대해서 다음의 식이 성립

$u_k(t)*u_r(t)=u_{k+r}(t)$

• 위와 같이 컨벌루션 하에서 특이함수를 정의함으로써, 특이함수들을 상대적으로 쉽게 이용 가능 + LTI 시스템에 대한 특이함수의 중요성 관점에서 그것들을 해석할 수 있다