신호 및 시스템 Chapt 1

Alan V. Oppenheim, Signals and Systems 책 내용입니다.

1. 신호와 시스템

1.1 연속시간 신호와 이산시간 신호

1.1.1 예와 수학적 표현

• 신호 : 정보를 담고 있음. 정보는 하나의 패턴으로 나타남
• 신호는 한 개 이상의 독립적인 변수들의 함수들로 표현됨

연속시간 신호(Continuous-Time Signal) : 독립변수가 연속적

• 독립변수 t 사용
• 괄호 ( $\cdot$ )

  이산시간 신호(Discrete-Time Signal) : 독립변수가 이산적

• 독립변수 n 사용
• 괄호 [ $\cdot$ ] 사용
• 오직 정수값에 대해서만 정의되어 있음 $\rightarrow$ $x[n]$을 이산순차열(discrete-time sequence) 또는 순차열(sequence) 이라고 불림
• 통계적인 데이터 신호들은 모두 이산시간 신호임

1.1.2 신호 에너지와 파워

신호 에너지

• 연속시간 : $E_{\infty}=\int_{-\infty}^{+\infty} |x(t)|^2 dt$
• 이산시간 : $E_{\infty}=\Sigma_{n=-\infty}^{+\infty} |x[n]|^2$

평균 파워

• 연속시간 : $P_{\infty}=\lim_{T\to\infty} \frac{1}{2T}\int_{-T}^{+T} |x(t)|^2 dt$

• 이산시간 : $P_{\infty}=\lim_{N\to\infty} \frac{1}{2N+1}\Sigma_{n=-N}^{+N} |x[n]|^2$

• 위의 정의들을 통해 신호는 3가지로 구분 가능

  (1) 유한 총 에너지를 가지는 신호들 $E_\infty < \infty \rightarrow P{\infty}=0$

  $\quad$ $P_{\infty}=\lim_{T\to\infty} \frac{E_\infty}{2T}=0$ 이기 때문

  (2) 유한한 평균 파워를 가지는 신호들 $P_{\infty}>0 \rightarrow E_\infty = \infty$

  (3) 무한한 평균 파워, 에너지 $P_{\infty}=\infty , E_\infty = \infty$

1.2 독립변수의 변환

• 신호와 시스템의 주된 개념은 변환임

  1.2.1 독립변수의 변환 예

  시간이동(time shift)

• $t_0, n_0$ 만큼 신호가 지연, 앞섬

  시간반전(time reversal)

• $t \rightarrow -t$ 또는 $n \rightarrow -n$

  시간 스케일링 (time scaling)

• $x(\alpha t )$ 또는 $x[\beta n]$
• 신호를 축소 또는 확장 하는 것

  일반적인 변환

• $x(\alpha t + \beta)$ 또는 $x[\alpha n +\beta]$

1.2.2 주기 신호(Periodic Signal)

• $x(t)=x(t+T)$ : 주기 T를 갖는 주기 신호(연속신호에서 정의)
• 기본 주기 $T_0$ : 위의 식을 만족하는 가장 작은 양의 $T$값
• $x[n]=x[n+N]$ : 주기 N를 갖는 주기 신호(이산신호에서 정의)
• 기본 주기 $N_0$ : 위의 식을 만족하는 가장 작은 양의 $N$값

1.2.3 우함수 신호와 기함수 신호

• 우함수 신호 $x(-t)=x(t)$, $x[-n]=x[n]$
• 기함수 신호 $x(-t)=-x(t)$, $x[-n]=-x[n]$
  • 기함수 신호는 t=0에서 0임
• 모든 신호는 기함수, 우함수 신호들로 분리됨 $x(t)=\frac{1}{2} [x(t)+x(-t)]+\frac{1}{2}[x(t)-x(-t)]$

1.3 지수신호와 정현파신호

1.3.1 연속시간 복소지수신호와 정현파신호

복소지수신호

$x(t)=Ce^{at}$

• C와 a는 복소수임

Case 1. 실지수신호 : C와 a가 실수

• 아래의 두가지 형태로 존재

Case 2. 주기적인 복소지수신호와 정현파 신호 : a가 순수 허수

• 이 신호는 주기적임 $x(t)=Ce^{jw_0(t)}=Ce^{jw_0(t+T)}$
• 주기적이기 때문에 $e^{jw_0T}=1$
• 최소 기본주기는 다음 값과 같음 $\rightarrow$ 기본주파수는 기본주기에 반비례 $T_0= \frac{2\pi}{|w_0|}$
• 오일러 관계(Euler’s relation) 에 따르면 위 신호들은 정현파 신호로 변환 가능 $x(t)=Acos(w_0 t+\phi)=\frac{A}{2}e^{j\phi}e^{j w_0 t}+\frac{A}{2}e^{-j\phi}e^{-j w_0 t}$
• 해당 신호는 무한한 에너지, 유한한 평균 파워를 가지는 신호의 중요한 예
• 복소지수 $e^{jwt}$가 주기 $T_0$를 갖기 위해서는 $e^{jwT_0}=1$ $wT_0=2\pi k \quad (k=0,\pm1,\pm2 \cdots)$
• 즉 $w$는 $w_0$의 정수배

  Case 3. 일반적인 복소지수신호

  $C=|C|e^{j\theta},a=r+jw_0$

• 즉 함수는 다음과 같이 표현 가능 $x(t)=Ce^{at}=|C|e^{rt}(cos(w_0 t +\theta)+jsin(w_0 t+\theta))$

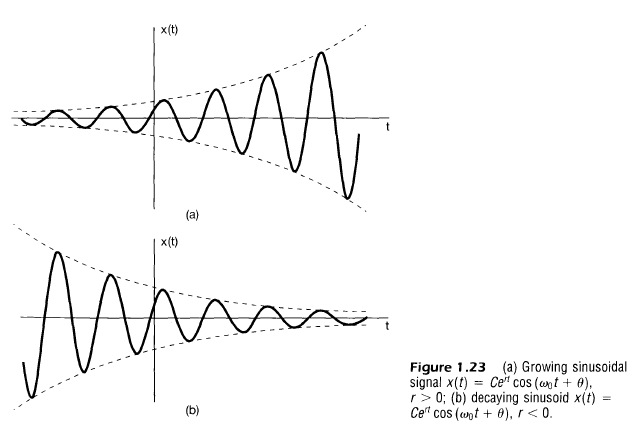
• 아래 그래프의 포락선은 복소지수의 크기와 동일 즉 $\pm

  C

  e^{rt}$

• r>0일 시 증가하는 정현파, r<0일 시 감소하는 정현파

1.3.2 이산시간 복소지수 및 정현파 신호

• 복소지수신호 or 순차열 $x[n]=C\alpha^n$
• 또한 다음과 같은 형식으로 표현 가능 $x[n]=Ce^{\beta n}$
• 둘 다 같은 의미($\alpha=e^\beta$) 위의 식으로 표현하는 것이 더 편리

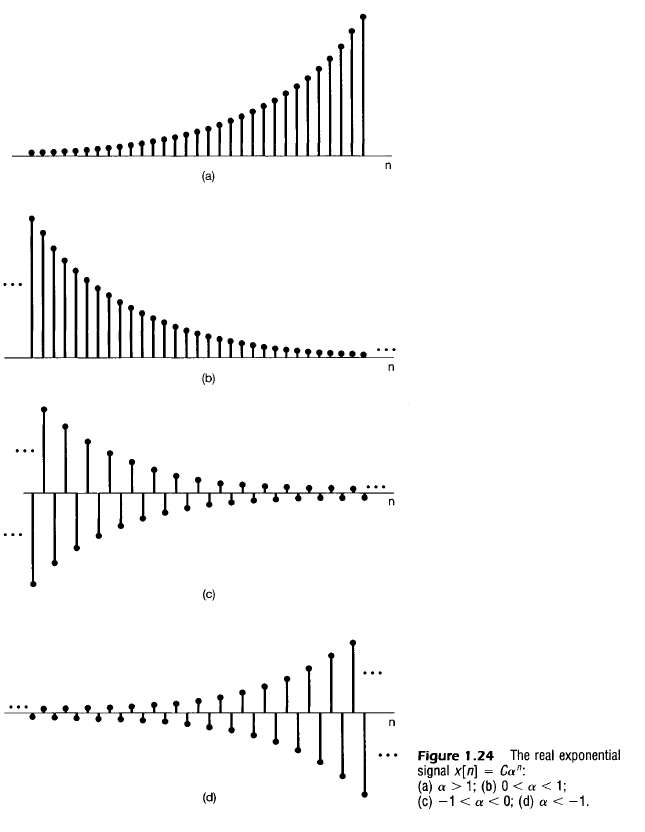
Case 1. 실지수신호 : C와 a가 실수

• 아래의 4가지 형태로 존재
• $\alpha$의 값이 음수이면 x[n]의 부호는 번갈아 바뀜(c,d)
• 나머지는 연속상황과 비슷함

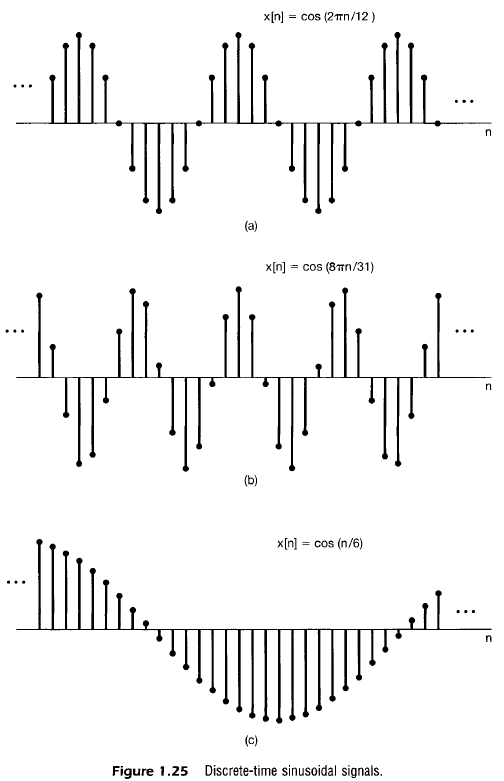
Case 2. 정현파 신호 : $\beta$가 순수 허수 $\leftrightarrow |\alpha|=1$

• 이 신호는 주기적임 $x[n]=Acos({w_0 n+\phi})=Ce^{jw_0(t+T)}$
• 오일러 관계(Euler’s relation) 에 따르면 위 신호들은 정현파 신호로 변환 가능 $x(t)=Acos(w_0 n+\phi)=\frac{A}{2}e^{j\phi}e^{j w_0 n}+\frac{A}{2}e^{-j\phi}e^{-j w_0 n}$
• 해당 신호는 무한한 에너지, 유한한 평균 파워를 가지는 이산신호의 중요한 예

  Case 3. 일반적인 복소지수신호

  $C=|C|e^{j\theta}$ $a=|a|e^{jw_0}$

• 즉 함수는 다음과 같이 표현 가능 $x(t)=Ce^{at}=|C||a|^n(cos(w_0 n +\theta)+jsin(w_0 n+\theta))$

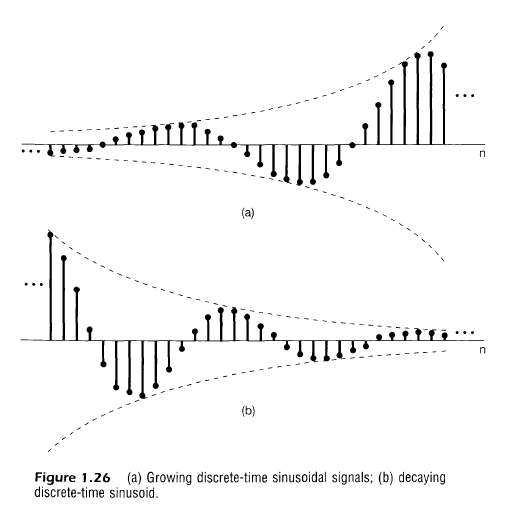
• a	=1일때 복소 지수열의 실수와 허수 부분은 정현파

• a	<1일때 지수적으로 감쇠하는 걸로 곱해짐

• |a|>1일때는 지수적으로 증가하는 것으로 곱해짐

1.3.3 이산시간 복소지수의 주기 특성

• 연속신호 $e^{jw_0t}$의 특징

$\quad$ (1) $w_0$의 크기가 커질수록 신호에서 진동의 비율은 높아진다

$\quad$ (2) 어떤 $w_0$값에 대해서도 주기적

• 이산신호에는 성립하지 않음

$\quad$ ex) 이산신호에는 $e^{j(w_0+2\pi)n}=e^{jw_0 n}e^{2\pi n}=e^{jw_0 n}$

$\quad$ $w_0+2\pi$인 지수는 주파수가 $w_0$과 같음 $\rightarrow$ 연속시간의 경우와 매우 다른 상황 발생

즉 이산시간 복소지수를 고려할 때는 $2\pi$ 길이의 주파수 구간만 고려하면 됨

• 위의 특성 때문에 아래 그림에서 $w_0$을 0에서 $\pi$까지 증가시키면 신호는 더 급속하게 진동하지만, $\pi$에서 $2\pi$까지 이르면 진동률은 감소한다

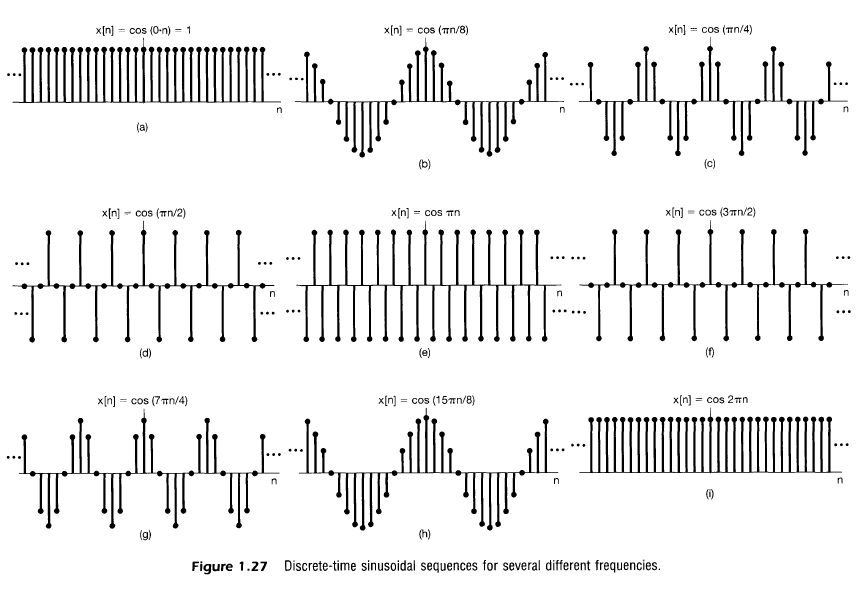
• 이산 복소지수의 주기가 N이 되기 위해서 아래의 식이 성립해야 함 $e^{jw_0(n+N)}=e^{jw_0 n}$ $w_0 N=2\pi m \rightarrow \frac{w_0}{2\pi}=\frac{m}{N}$

  즉 이산시간 복소지수를 고려할 때 $w_0/2\pi$가 유리수가 나와야지 주기적, 그렇지 않으면 주기적이지 않음(ex. 1.25(c))

• 위의 식을 통해 (주기를 아는 경우) 신호의 기본주파수는 다음과 같이 구할 수 있음 $\frac{2\pi}{N}=\frac{w_0}{m}$

내용 정리하면 아래의 표와 같음

ex) $cos[8\pi n/31]$의 주기 $T=31$, $w_0=8/31$, 기본주파수=1/31

• 주기함수이므로 $\phi_k[n]=e^{jk(2\pi/N)n} \quad (k=0,\pm 1, \pm 2, \cdots)$
• 위와 같이 주어진 집합에서 구별되는 주기 지수들은 단지 N개뿐(0,1, … , N-1)

1.4 단위 임펄스 및 단위 계단 함수

1.4.1 이산시간 단위 임펄스 및 단위 계단 순차열(sequence)

단위 임펄스 (Unit Impulse)

$\delta[n]=\begin{cases} 0, \quad n\neq 0 \\1, \quad n=0 \end{cases}$

단위 계단 (Unit Step)

$u[n]=\begin{cases} 0, \quad n < 0 \\1, \quad n\geq 0 \end{cases}$

• 둘 사이의 관계 $\delta[n]=u[n]-u[n-1]$ $u[n]=\sum_{m=-\infty}^n \delta[m]$

• 다음과 같이 변형 가능 $u[n]=\sum_{k=-\infty}^0 \delta[n-k]$

• 중요한 샘플링 특성을 가짐 $x[n]\delta[n]=x[0]\delta[n]$ $x[n]\delta[n-n_0]=x[n_0]\delta[n-n_0]$

1.4.2 연속시간 단위 임펄스 및 계단 함수

단위 계단 (Unit Step)

$u(t)=\begin{cases} 0, \quad t < 0 \\1, \quad t\geq 0 \end{cases}$

단위 임펄스 (Unit Impulse)

$\delta(t)=\begin{cases} 0, \quad n\neq 0 \\1, \quad n=0 \end{cases}$

• 둘 사이의 관계 $u(t)=\int_{-\infty}^t \delta(\tau)d\tau$ $\delta(t)=\frac{du(t)}{dt}$

• But 불연속이므로 두 번째 성질을 적용하는데 문제가 발생
• 새롭게 정의(근사함수) $\delta(t)=\lim_{\Delta\to\infty}\delta_\Delta(t)$

  단위 임펄스 (Unit Impulse)

  

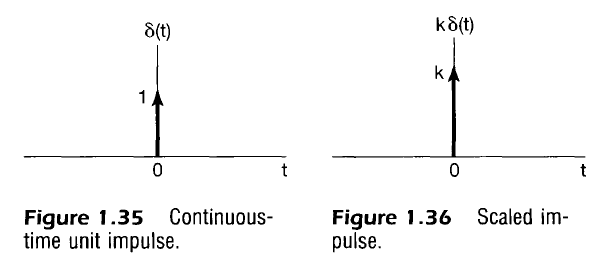
• 크기 “1”은 임펄스의 면적을 나타내기 위해 사용됨
• 비율 변화된 임펄스는 면적이 k이며 다음과 같이 정의 $\int_{-\infty}^t k\delta(\tau)d\tau=ku(t)$

  함수간의 관계를 다음과 같이 표시 가능(중요, 샘플링과 연결)

  $u(t)=\int_{-\infty}^t \delta(\tau)d\tau=\int_{\infty}^0\delta(t-\sigma)d\sigma$

• 연속시간 임펄스도 중요한 샘플링 특성 존재 $x(t)\delta(t)=x(0)\delta(t)$ $x(t)\delta(t-t_0)=x(t_0)\delta(t-t_0)$

• 단위 임펄스는 이상화해서 정의한 것
• 실제 물리적 시스템은 관성이 있어서 입력에 대한 즉각적인 반응이 불가
• 즉 이렇게 짧은 펄스의 시스템 응답은 눈에 띌만한 영향을 주지 못함
• 그러나 펄스의 중요한 특징은 그 적분된 영역임
• 더이상 펄스의 형태나 구간이 문제가 되지 않기 전에 보다 짧은 펄스를 찾을 수 있음
• 단위 임펄스 : 어떠한 시스템에 대해 충분히 짧은 펄스
• 2.5장의 singulary function 쪽을 보면서 다시 복습해볼것
• 예제 1.7의 신호 복구를 보면 보다 잘 이해 가능

1.5 연속시간 및 이산시간 시스템

• 입력 신호가 시스템에 의해 변환되거나, 시스템에 의해서 응답되도록 해서 출력을 내게 하는 것을 의미

  연속시간 시스템

• 연속적인 입력 신호가 가해져 연속적인 출력 신호가 나오는 시스템 $x(t) \rightarrow y(t)$

  이산시간 시스템

• 이산적인 입력 신호가 가해져 이산시간 출력 신호가 나오는 시스템 $x[n] \rightarrow y[n]$

• 일반적으로 서로의 관계가 미분방정식 형태로 나타내짐
• 시스템에 대한 수학적인 표현을 위해서는 시스템을 두가지 특성을 가지고 있다고 인지해야 함 (1) 시스템은 우리가 분석을 하기 위해서 추출할 수 있는 구조와 성질을 가지고 있음 (2) 많은 실질적인 중요성을 갖는 시스템은 이러한 방식으로 정확히 모델링 될 수 있음

1.5.2 시스템의 상호연결(Interconnection)

• 직렬(Cascade) 상호연결
• 병렬(parallel) 상호연결

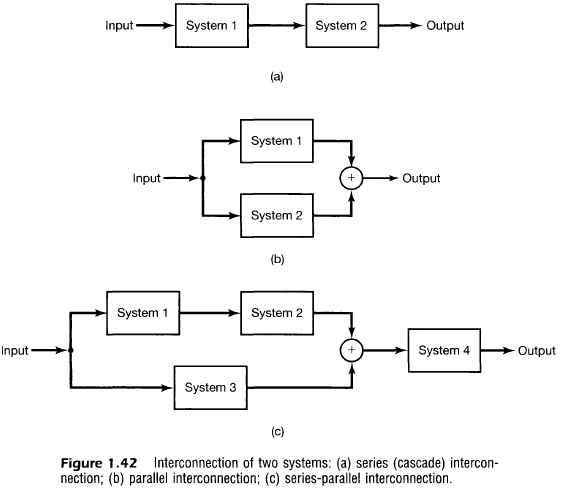
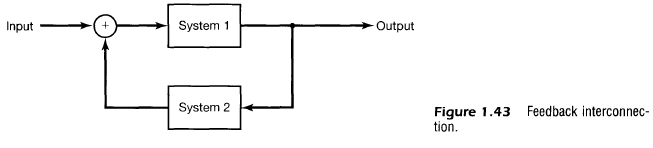
• 피드백(Feedback) 상호연결

1.6 기본적인 시스템 특성

1.6.1 메모리 시스템과 없는 시스템(Memoryless system)

메모리없는 시스템(Memoryless)

• 출력이 같은시간에 입력에만 의존할 때
• ex) 항등(identity system) $y(t)=x(t), y[n]=x[n]$

  메모리 시스템 (memory system)

• 지난 시간 또는 이후 시간 데이터에도 의존
• ex) 누산기, 합산기, 지연기 $y[n]=x[n-1]$

1.6.2 가역성(Invertibility)와 역시스템(Inverse system)

가역적(invertible)

• 별개의 입력에 대해 별개의 출력이 나옴
• 가역적이면 역시스템이 존재함
• 비가역적인 시스템의 예 $y[n]=0$

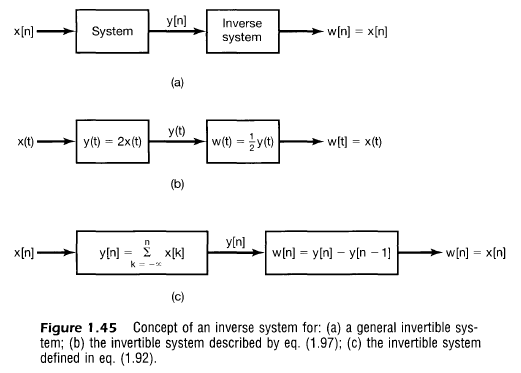
• 통신에서 중요함. 원래의 메세지를 코드화 하는 과정에서(인코딩) 신호에 중복성을 주어 전송 과정에서 발생할 수 있는 에러를 검출하고 가능하면 정정
• 손실이 없는 코딩(lossless coding)을 위해서는 출력에서 입력을 정확하게 재생할 수 있어야 됨

1.6.3 인과성(Causality)

• 시스템의 출력이 현재와 과거값에만 의존
• 비인과적인 시스템은 구간 좌우로 평균을 출력으로 하는 시스템(Moving Average)

1.6.4 안정성(Stability)

• 작은 입력에 대해서 출력이 발산하도록 하지 않는 성질
• 그림에서 위가 안정한 진자, 아래가 불안정한 역진자

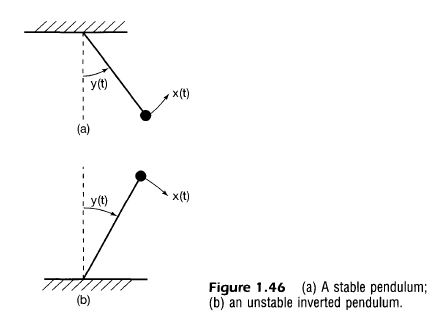
정리하자면 입력의 크기가 제한이 된다면 출력도 제한되어야 함(발산하지 않음)

1.6.5 시불변성(Time Invariance)

• 시스템의 행동과 특성이 시간에 고정되어 있는 시스템

• 즉 시간을 변경했을 때 시스템 응답이 동일하게 변환되는지 확인하면 됨 $if \quad x[n] \rightarrow y[n] \quad then \quad x[n-n_0] \rightarrow y[n-n_0]$

• 시불변 시스템이 아닌 중요한 예가 시간 스케일(Time-scaling) 시스템

1.6.6 선형성(Linearity)

• 중첩 특성을 만족하는 시스템(선형대수학)

(1) 가산성(additivity) : $x_1(t)+x_2(t)$에 대한 응답은 $y_1(t)+y_2(t)$

(2) 동질성(homogeity) : $ax_1(t)$에 대한 응답은 $ay_1(t)$, 여기서 a는 임의의 복소 상수

연속시간 : $ax_1(t)+bx_2(t) \rightarrow ay_1(t)+by_2(t)$

이산시간 : $ax_1[n]+bx_2[n] \rightarrow ay_1[n]+by_2[n]$

• 모든 시간에서 0인 입력은 모든 시간에서 0인 출력을 야기함(동질성) $0=0\cdot x[n] \rightarrow y[n]=0$

1.7 정리

• 이후 이 책에서 중요한 관심은 연속시간, 이산시간 모두 선형 시불변 시스템(LTI system)에 집중될 것