오토인코더의 모든 것

오토인코더의 모든 것 Naver(이활석) 강연자 강의 정리내용입니다.

(https://www.youtube.com/watch?v=o_peo6U7IRM)

키워드

• unsupervised learning
• Nonlinear Dimensionality reduction
  • Representation learning
  • Efficient coding learning
  • Feature extraction
  • Manifold learning
    • 인코더는 차원 축소의 역활
• Generative model learning
  • Variational autoe ncoder 가 나오면서 발전됨
  • 디코더는 생성 모델의 역활
• ML density estimation

1. 딥 뉴럴넷을 학습과 관련해서

• ML density estimation을 하는 것
• 기존의 머신러닝과 차이점
  • 기존의 머신러닝 기법은 모델 $f_\theta(x)$ 를 선택함(트리, SVM 등등)
  • 딥 뉴럴넷은 모델 $f_\theta(x)$ 를 딥 뉴럴 네트워크를 사용함
    • 이 때는 Loss function의 제약 조건이 걸리게 됨(MSE, CrossEntropy등밖에 사용 못함)
    • 이는 Backpropagation 알고리즘을 사용하기 때문임
    • 역전파를 하기 위한 두가지 가정
      • 전체에 대한 Loss function은 각 sample별 loss의 합과 같다
      • Loss function과 네트워크의 출력값과 정답 값만 가지고 구성한다
  • Gradient descent를 통해 최적의 파라미터를 구함
    • Iterative method로써 step별로 Loss 값을 줄이는 방향으로 진행
    • 이를 위해서 Tayler expansion을 사용하여 근사하는 방법 사용
      • Sample point에서 약깐만 이동할 때 잘 맞음(Learning rate를 작게 설정하는 이유)
    • 전체 평균을 구하기 어렵기 때문에 일반적으로는 일부(batch)의 gradient를 구해서 진행하는 Stochastic Gradient Descent를 사용함
• Loss function의 해석
  • Backpropagation관점에서은 cross entropy에서 더 잘 작용함
    • 초기값에 둔감함(Gradient Vanishing Problem이 적음, Activation Function의 미분항이 없기 때문임)
  • Maximum likelihood관점에는 Discrete는 Cross entropy Continuous는 MSE가 더 잘 맞는다

    • Cross Entropy는 $p(y

      f_\theta (x))$을 Maximize하는 것으로 해석

    • I.I.D condition 가정
      • Independence : 모든 데이터는 서로서로 독립 $\ p(y|f_\theta (x))=\Pi_i p_{D_i}(y|f_\theta (x_i))$
      • Identical Distribution : 우리의 데이터는 동일하게 분포되어 있음 $\ p(y|f_\theta (x))=\Pi_i p(y|f_\theta (x_i))$
    • 따라서 Density estimation으로 Sampling도 가능함
    • 확률 분포를 Gaussian 분포로 가정 시 MSE값이, Bernoulli 분포로 가정 시 Cross-entropy가 나옴

    • 참고 : Maximum likelihood 관점에서는 Network의 출력값이 likelihood인 $p(y_i

      x_i)$가 아님

      • Gaussian Distribution(MSE)에는 함수의 평균값 $f_\theta (x_i)=\mu_i$ 이며
      • Categorical Distribution(Cross-entropy)에는 분포의 확률값 $f_\theta (x_i)=p_i$이다
    • 참고 : Log-likelihood for Neural Nets

      • 조건부 확률인 $P(Y

        X)$를 추정하는 것

      • 이는 다음과 같이 출력값으로 파라미터화 됨 $P(Y

        X)=P(Y

        w=f_\theta(X))$

      • $Loss = -log P(Y

        X)$

        • Gaussian : MSE
        • Multinoulli : softmax
• 오토인코더 vs Variational Autoencoder

  • 오토인코더의 확률분포 : $p(x

    x)$

  • VAE의 확률분포 : $p(x)$

2. Manifold Learning

• Manifold 정의 : 고차원의 데이터를 error없이 잘 아우르는 subspace
• Manifold를 잘 projection 시키면 데이터의 차원이 줄어들 수 있다고 생각하는 방식

• 용도

  1. Data compression
  2. Data visualization(포장 , 3D)
  3. Curse of dimensionality (대부분의 이유 1)
     • 차원이 커질수록 필요한 데이터 샘플의 수가 늘어난다.
  4. Discovering most important features (대부분의 이유 2 :특성 공학)
• Manifold Hypothesis
  • 고차원의 데이터의 밀도는 낮지만, 이들의 집합을 포함하는 저차원의 manifold가 있음
  • 저차원의 매니폴드를 벗어나는 순간 밀도는 급격히 낮아진다
  • Dominant 한 feature들을 자동으로 찾아줘야 좋은 압축이다
  • Reasonable distance metric을 사용해야 함
    • 유클리디안 거리로 구하면 문제가 생길 수 있음.
    • Manifold의 거리를 고려해야 할 것
  • Manifold를 disentangle 한다고 함
  • Dimensionality Reduction의 다른 방법들
    • Linear
      • PCA
        • 분산이 최대가 되는 plane을 찾아가면서 projection 해나가는 것
        • 꼬여있는 애들은 잘 disentangle하지 못함
      • LDA
    • Nonlinear
      • Autoencoder
      • t-sne
      • LLE
        • 1. 가까운 데이터 포인터를 먼저 찾는다 (K-NN)
  • 확인해 보면 기존의 방식들은 Neighborhood based training이다.
  • 그러나 고차원 데이터 간의 유클리디안 거리는 유의미한 거리 개념이 아닐 수도 있기 때문에 Autoencoder가 더 좋다고 생각해 볼 수 있다.
  • 즉 데이터의 수가 많고 고차원일수록 오토인코더를 통한 차원 축소가 유의미하다고 할 수 있다.

3. 오토인코더

• 자기지도학습이라고 불림(스스로를 학습하니까)
• 생성된 데이터가 학습 데이터와 닮아 있다는 단점
  • 최소한의 성능은 보장된다는 장점이 되기도 함

Linear Autoencoder

• Activation function 없이 사는 것
• MSE를 쓰면 PCA와 똑같은 manifold를 배운다
• RBM은 요즘 안쓰니 패스~~

Stacking Autoencoder

• 처음에 오토인코더가 차원축소와 weight초기화로 많이 쓰였음
• 최근에는 weight초기화하기위한 pretrain model으로 안쓰임

Denoising Autoencoder

• 학습에 noise를 추가한 뒤 결과 값이 noise추가 이전의 데이터를 출력으로 하여 학습시키는 것
• noise를 약간만 추가하는 것 (ex. 사람이 같은 소리라고 생각할 정도의 noise)

Stacked Denoising Auto-Encoders

• 오토인코더로 pretraining한거랑 Stacking한 것이랑 성능 비교
• noise도 추가했을 때 pretrain이 더 잘되더라
• Generation도 잘된다

Stochastic Contractive Autoencoder(SCAE)

• 오토인코더에 noise없을 때와 추가했을 때와의 manifold상의 거리를 최소화 하는 항을 추가하는 것 $L_{SCAE}=\sum_{x\in D} L(x,g(h(x)))+\lambda E_{q(\tilde{x}|x)}[\ ||h(x))-h(\tilde{x})||^2 \ ]$

Contractive Autoencoder (CAE)

• Tayler expansion을 통해서 앞의 Stochastic Regularization term을 Analytic Term으로 변경한 것 $E_{q(\tilde{x}|x)}[\ ||h(x))-h(\tilde{x})||^2 \ ] \approx ||\frac{\partial h}{\partial x}(x))||^2_F$
• F는 프로비우스 평균임
• 최근에는 잘 안씀

Variational Autoencoders

• 압축 한 뒤 T-sne도 해봄.
  • 잘 압축이 되었다면 고전적인 visualization 방식을 했을 때 좋은 결과가 나올 것이기 때문(neighborhood)
• 실제로 오토인코더랑 별로 관련이 없음
• Generative 구조를 만들기 위해서 앞단이 공교롭게 오토인코더 구조였을 뿐
• 우리가 구하고 싶어하는 것은 p(x)
  • Marginalize 후 적분해서 구한다
• 따라서 prior값인 z 값을 우리가 고정하는 것
• 이렇게 고정해도 될까?
  • 한 두개 layer가 복잡한 것을 익히는데 사용될 수 있으므로 괜찮다(논문)
• Monte Carlo 방식으로 그냥 더하면 안되는 이유?
  • Prior 관점에서 Sampling을 해버리면 문제가 발생함
  • Likelihood을 높이기 위해 가우시안 분포에서 평균에 해당 되는 값이 MSE 값이 작은 데이터가 선택이 되는데 실제로는 같지 않을 확률이 있다.
  • 예시 : 그림의 숫자 2에 대해서 (a),(c)의 MSE가 (a)와 (b)의 MSE보다 크다.
• 즉 prior가 아닌 x가 주어졌을 때의 확률$P(z|x)$을 정하는 것이며 Variational Inference방법을 사용하는 것임
• 우리가 알고 있는 확률 분포중에서 True posterior과 가장 닮은 함수를 구해서 샘플링하는 것

• p(z

  x)를 구하기 힘들기 때문에 q_\phi (z

  x)를 도입해서 approximate 하는 것

• $p(x)$의 $ELBO(\phi)$(lower bound) 구하기
• 의미적으로 직관적인 방식
• 즉 분포를 비슷하게 맞춰준다는 것은 KL 값을 minimize 한다는 것이고 이는 ELBO를 Maximize하는 $\phi$를 찾는 것과 같다
• 최종적으로 Loss function은 두 항을 Maximize 하는 것과 같음
• Variational Inference : 이상적인 샘플링 함수를 찾는 것 = ELBO maximize 하는 $\phi$

• Maximum likelihood을 하는 $\theta$를 찾는 것

• 정리하자면 다음과 같다
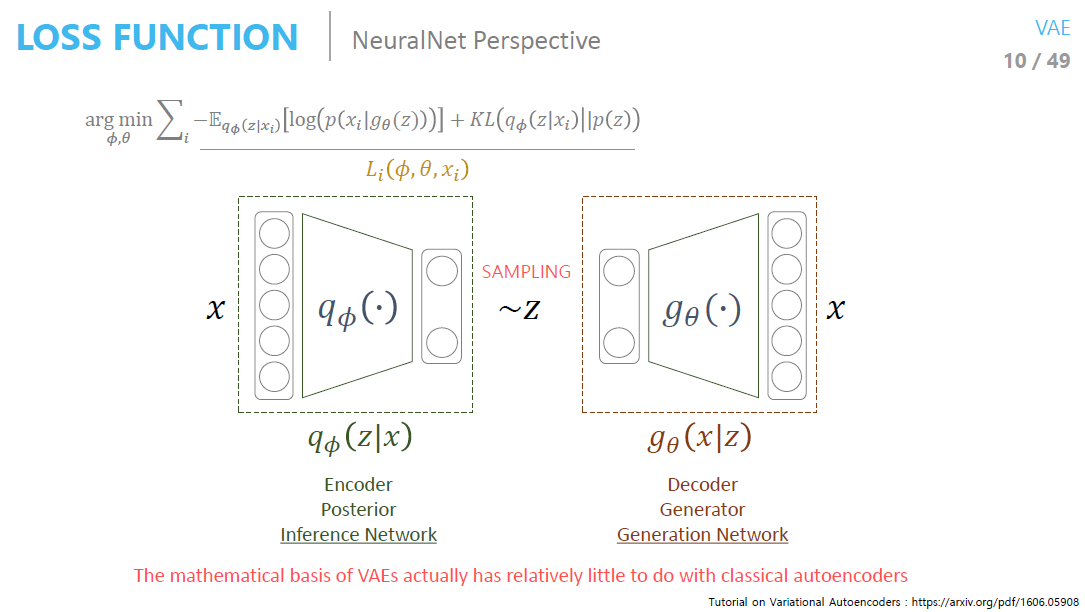
• 뒷단을 학습하기 위해서 앞단을 붙인 것
• Posterior을 sampling 하는 인코더

• 거기서 나온 z로 generation하는 디코더

• 엘보를 자세히 보면 Reconstruction term과 Regularization term으로 나눌 수 있음

• 그러면 prior p(z)를 평균이 0인 가우시안으로, $q_\phi (z|x)$도 가우시안으로 가정하고 진행하면 $\mu, \sigma$를 구해야 함
• But sampling시 중간 값이 랜덤으로 바뀌어서 역전파를 쓸 수 없음

• 중간 값을 바꾸는 방식을 사용 Reparameterize Trick

• 요약정리!
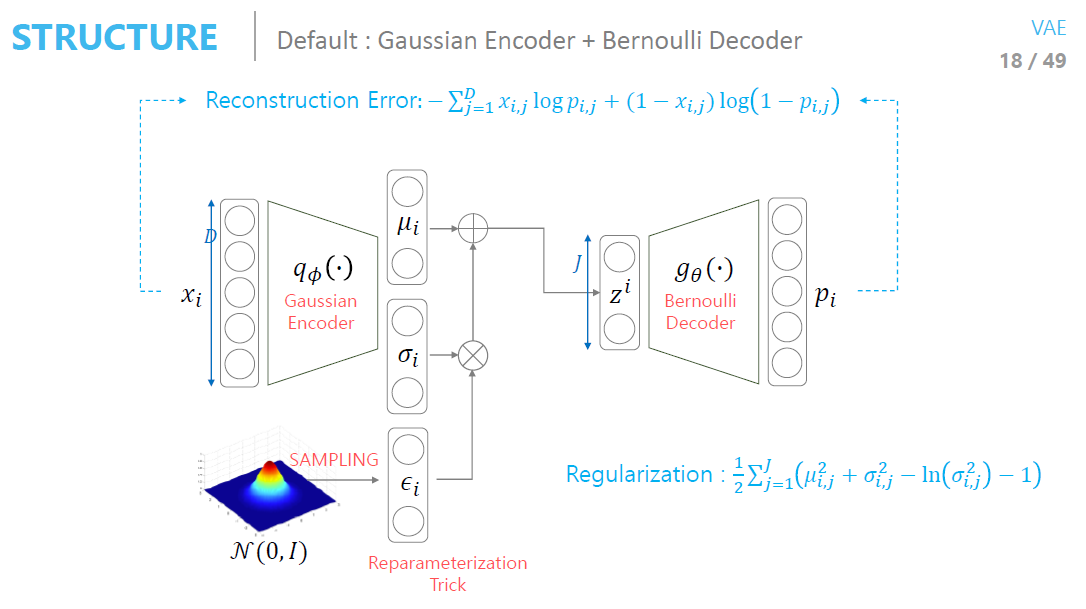
  • 사용한 분포에 따라서(Gaussian, Bernoulli) 결과가 약간 다름
• Manifold 관련해서는 오토인코더는 z 공간의 위치가 학습할 때마다 계속 바뀜
  • Generator 관점에서 매니폴드의 위치가 안정적이여야 좋음
• Feature가 잘 학습되어 있는 것을 확인할 수 있음.
• 전체 분포가 normal distribution을 따름

Conditional VAE

• 레이블 정보를 알고 있으면 레이블 정보를 넣어주는 것
• 그 때의 ELBO 식이 약깐 바뀜

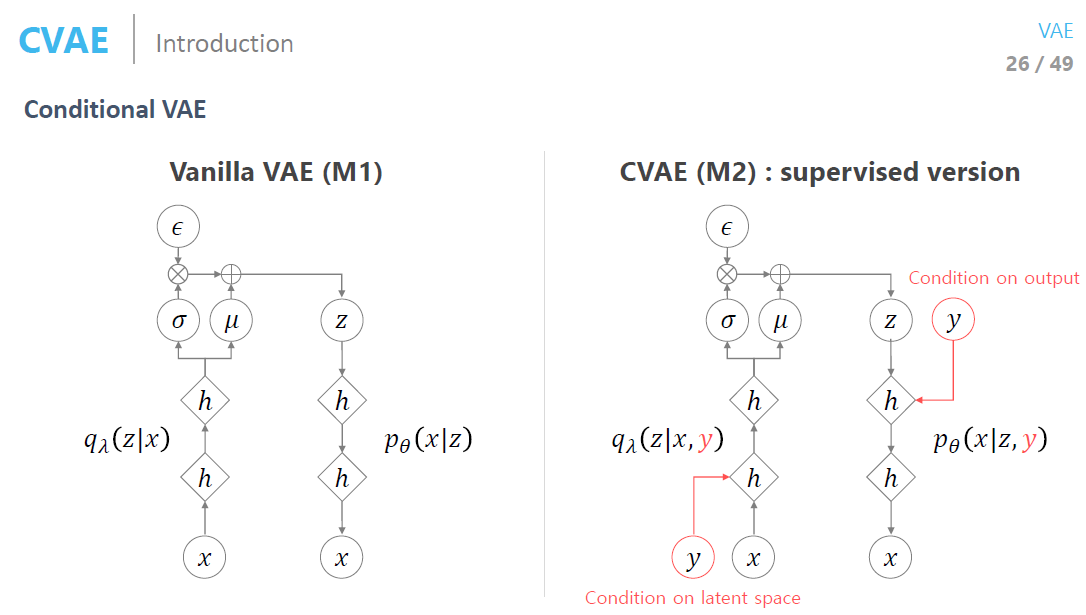
• CVAE의 많은 변형 버전들이 있음
• 추가적인 정보가 들어가기 때문에 빠르게 수렴함

Adversarial Autoencoder

• 기존 VAE의 Regularization 조건의 가정을 깨기 위해서 만듬
• KL 대신에 GAN loss를 사용하는 것
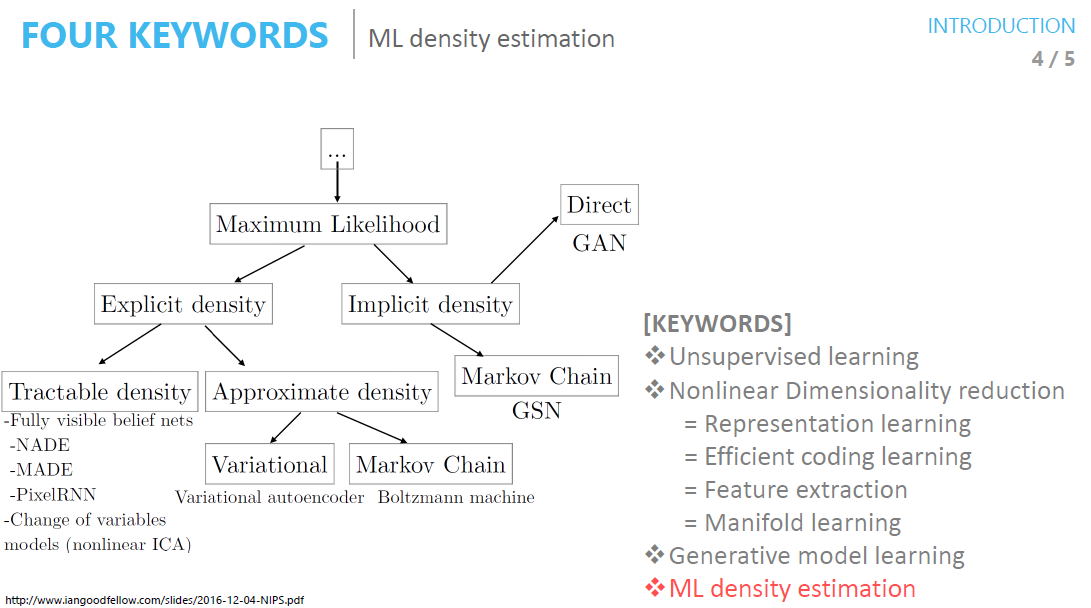
• Explicit density는 확률분포를 정해야 하지만 Implicit density는 확률분포를 안정해도 됨
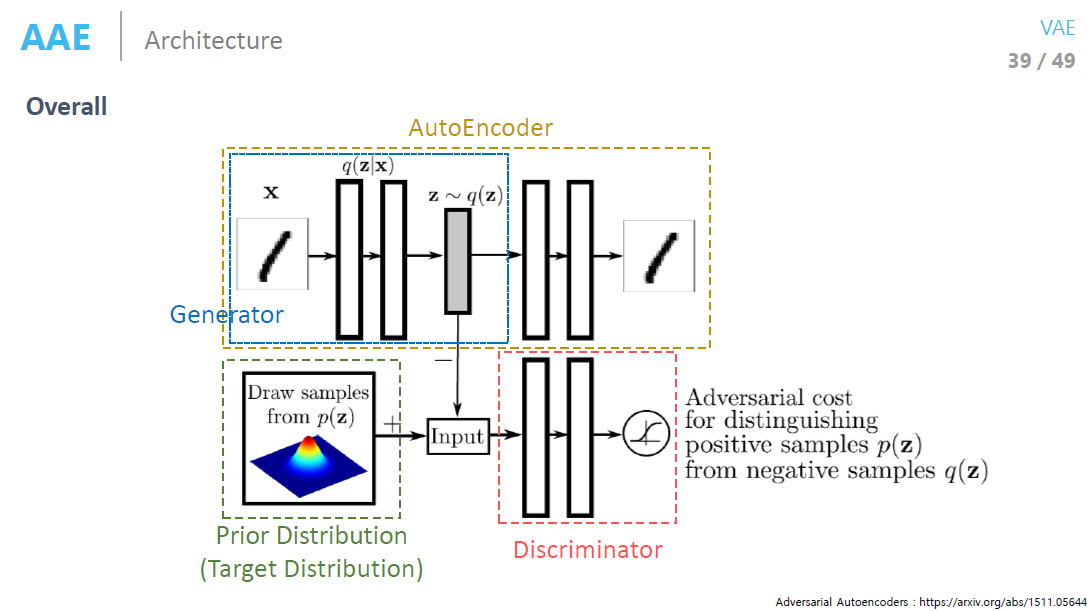
• 학습시킬때 Discriminator 한번 학습, Generator 한번 학습 서로서로 번갈아가면서 학습해야됨
• VAE와 비교해 봤을 때 Gan loss 때문에 좀더 prior 에 형태로 나와서 가우시한 형태 VAE는 MLE위주로 되어 있어 샘플 Distribution의 영향을 더 많이 받음
• 레이블 정보를 더 넣어주면(mapping) 진짜의 분포를 따라감
• AAE는 Manifold를 우리가 원하는 모양으로 만들 수 있다는 장점

Information Retrieval by Autoencoder

• Denoising Autoencoder가 VAE보다 Reconstruction 관점에서는 더 좋음(로스 텀이 Reconstruction 뿐이므로)
• VAE는 loss의 평균 값을 계산하기 때문에 이미지를 넣을 때Blurry하기도 한다

VAE vs GAN

• 생성 모델을 형성, 확률 분포를 추정한다는 점은 같다

• 방법이 전혀 다름

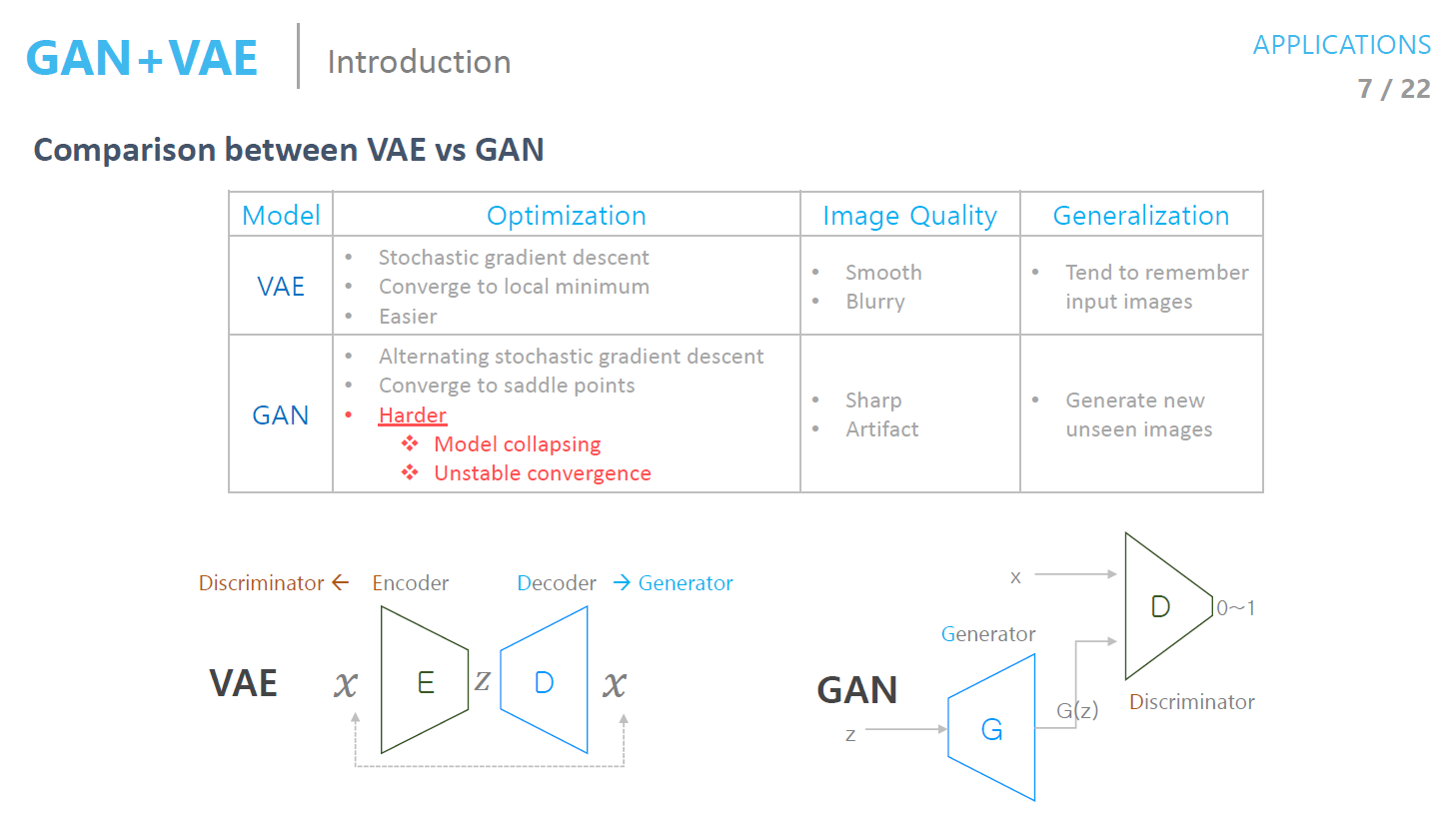
• VAE와 GAN을 구별하는 예제
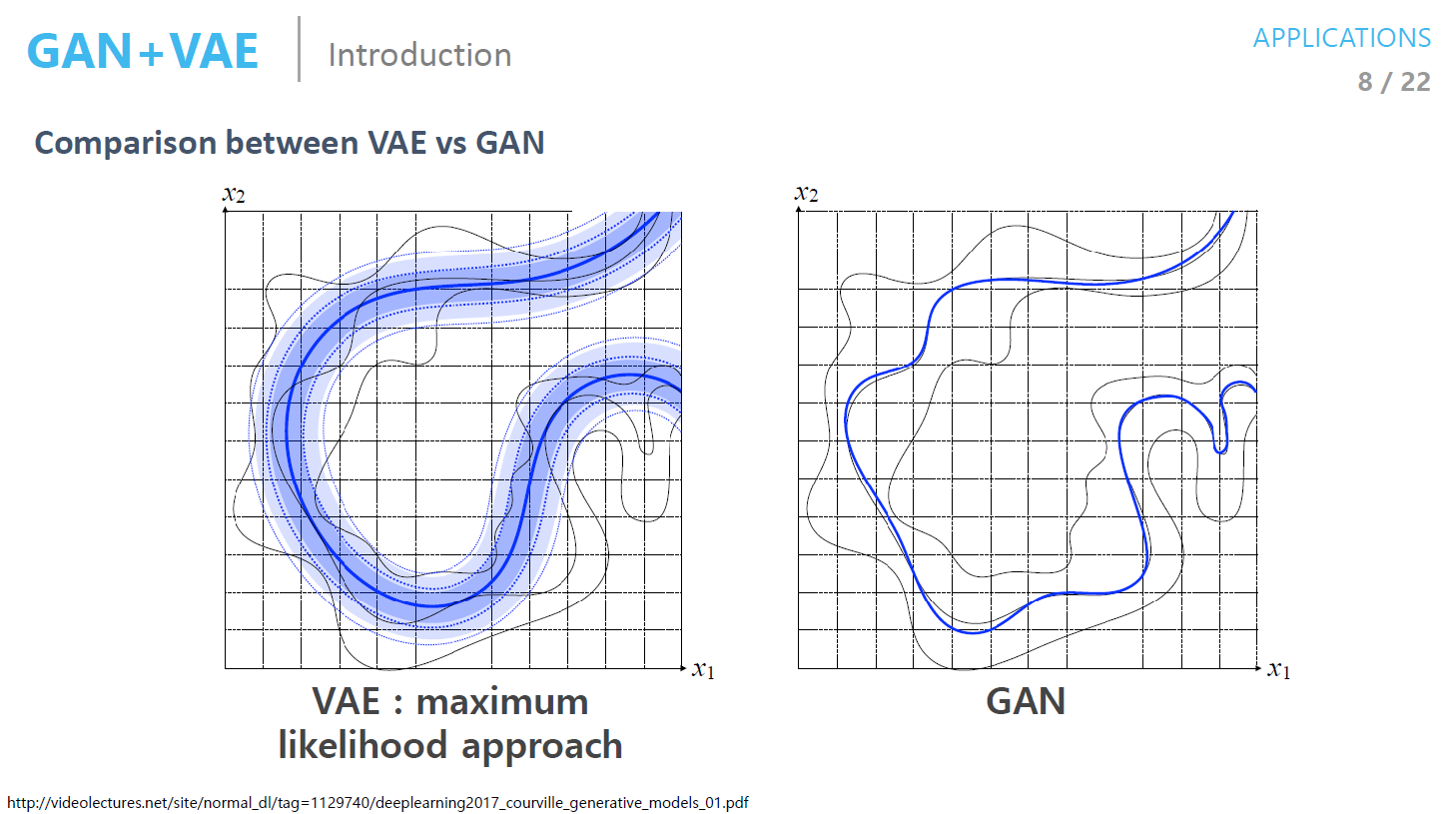
  • 한가지 모드의 데이터를 학습한 generator가 만든 샘플은 GAN은 진짜와 똑같으므로 학습이 끝남 (mode collapse)
  • 즉 보다 다양한 애들이 나오지는 않음
  • VAE는 데이터의 중간부분에도 나오므로 blurry
• GAN 논문은 두종류
  • GAN application
  • GAN의 학습을 보다 잘하게 하는 법

GAN + VAE

• EBGAN, BEGAN : Discriminator 를 오토인코더로 넣어서 실제 데이터면 reconstruction error를 높게, 다른 데이터면 reconstruction을 낮게 함

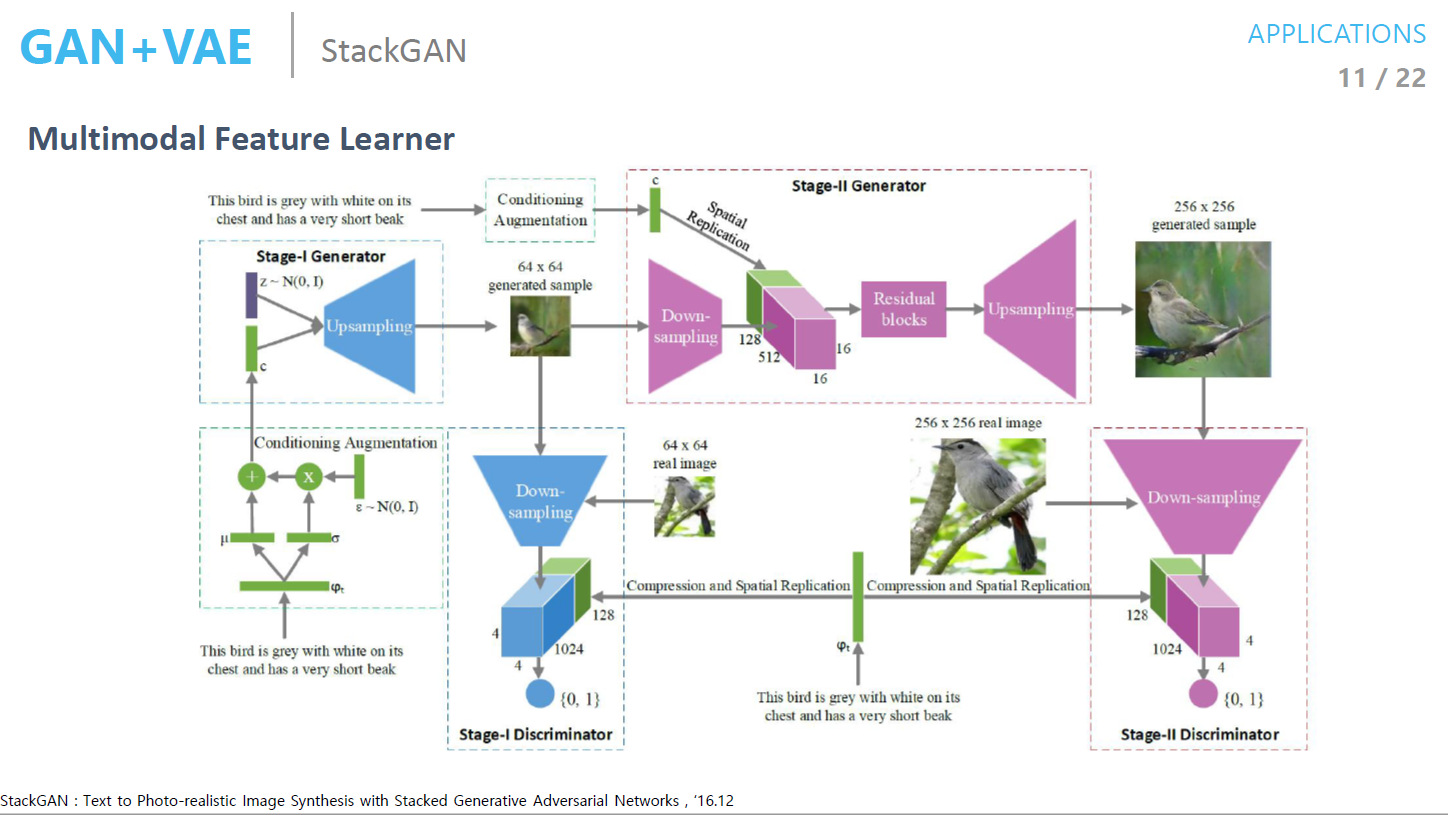
StackGAN

• VAE 학습을 한 뒤 인코딩 부분만 가져다가 쓴 것
• 랜덤 noise를 넣어서 이미지를 generate함
• 그 뒤에 다시 downsample 하여 문장 압축한 code와 같이 넣으면 이미지가 나오고 Reconstruction loss 구한 것

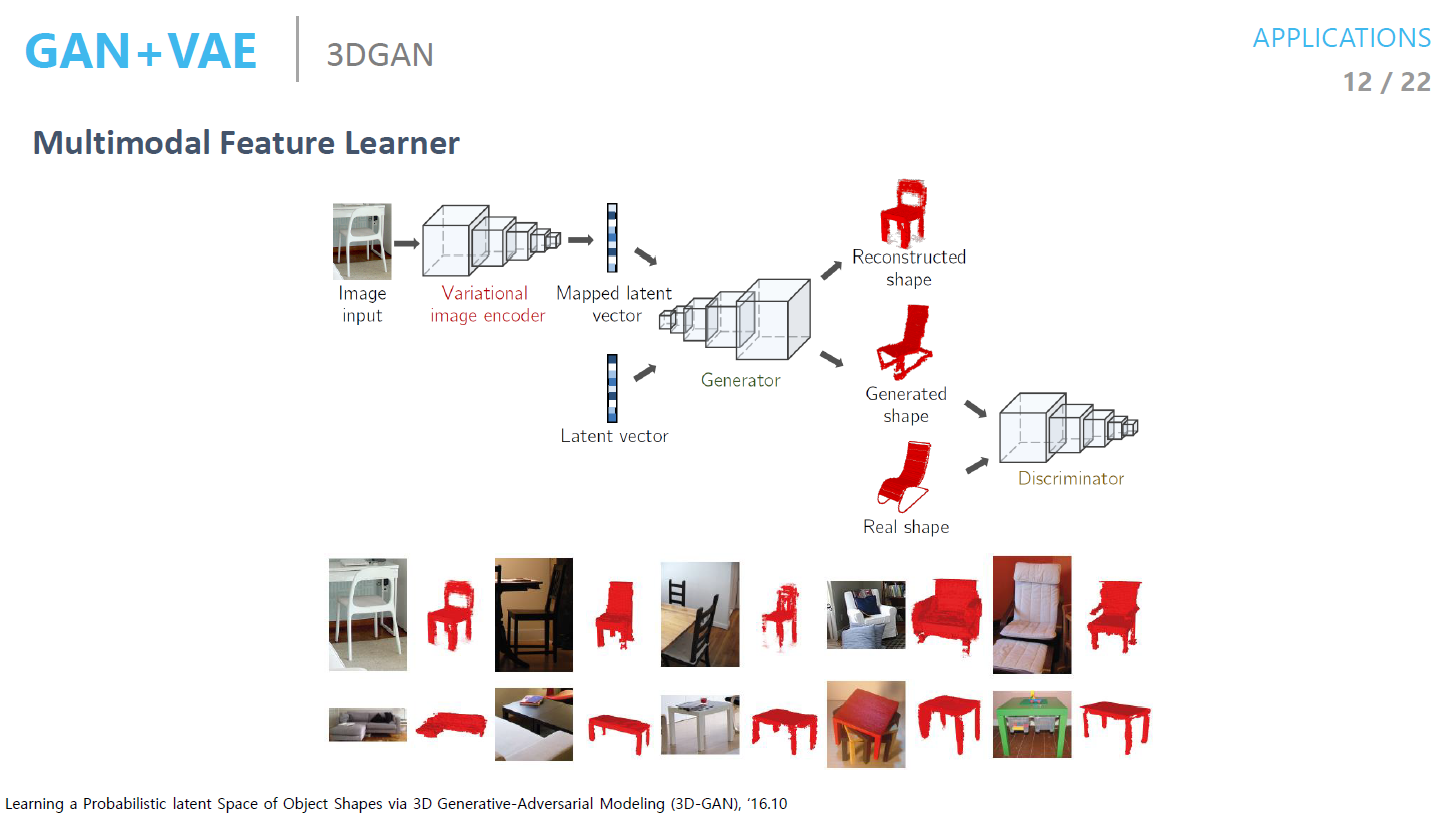
3D GAN

• 2D image에 대한 feature를 잘 뽑기 위해서 VAE로 학습을 하고 랜덤 벡터를 넣어서 이미지를 넣고 Discriminator를 사용하는 것

SEGAN

• Denoising Variational Autoencoder을 사용해서 본 뒤 Generated 된 결과가 진짜랑 가짜랑 비슷한지 비교해 보는 것
• 배경 노이즈 제거하는 것

Age Progression

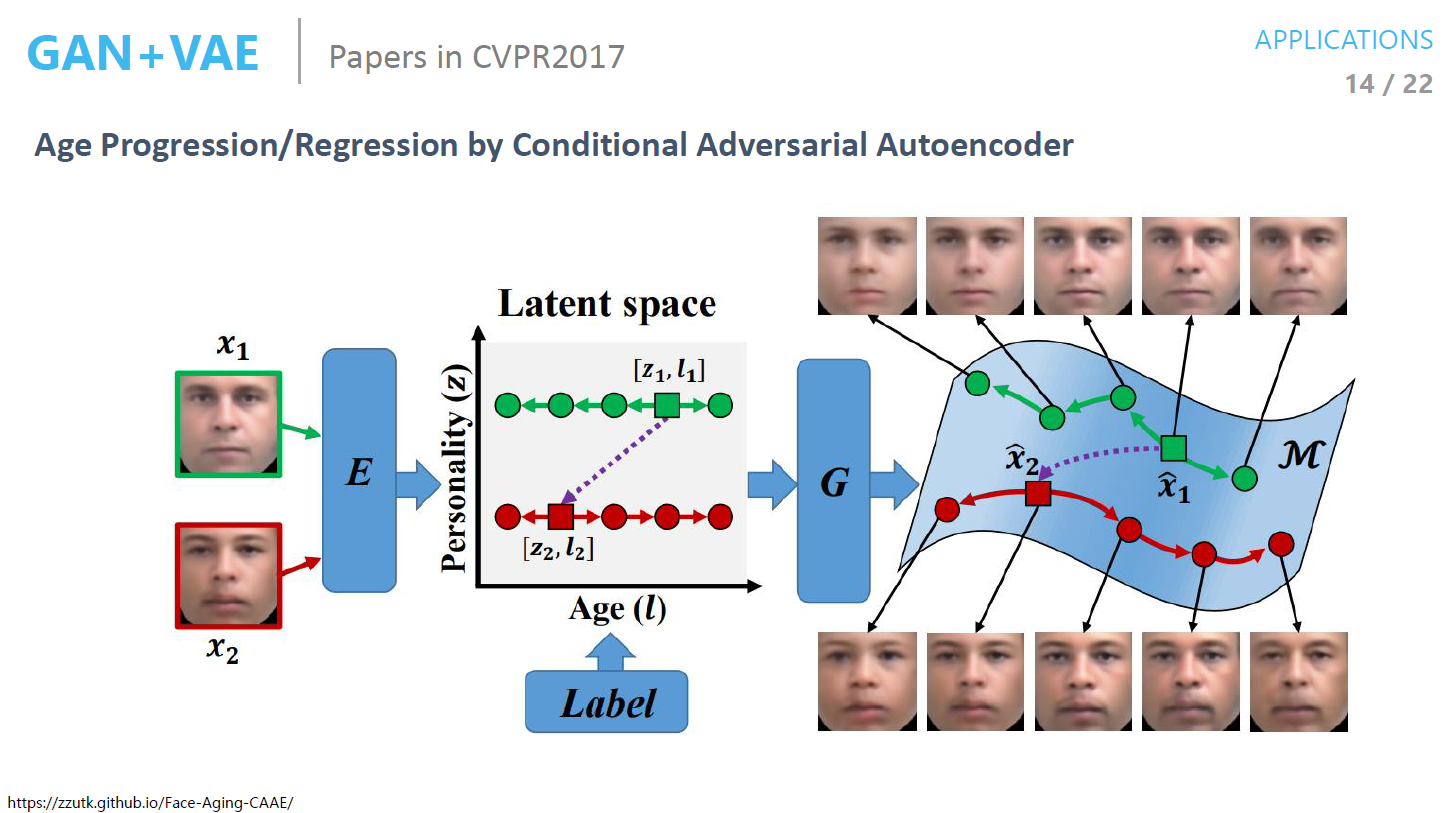
• Generation된 결과에 label을 넣어서 Reconstruct 하는 것

PalleteNet

• 이미지를 구성하는 주요 색상 팔레트만 바꿨을 대 채색을 다시하는 것
• Pallet을 Condition으로 줘서 ad만 바궈야 함

Noisy face Image halluciating

• 이미지 복원

Conditional Generation

• 실사 사진에 대해서 포즈 Condition에 대한 Image를 Generate 하는 것

정리

• VAE로 압축 후 Condition으로 넣어주는 경우가 많고 Generate해서 실제 데이터와 비슷한지 확인
• GAN 은 암흑기에 있고 발전이 암흑기에 있음
• 계속해서 발전해야 할 예정