기계학습_lec4_AAILab
Updated:
참고- 문일철 교수님 유튜브-AAiKaist \ (https://www.youtube.com/watch?v=sDG1Y1vxOjs&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=2)
(새롭게 알게된 정보들만 자세히 기술, 나머지 내용들은 간략하게 정리함)
Logistic Regression

- 앞에서 얘기한 것처럼 실선 부분이 더 좋은 Classifier
- 반달 모양의 Risk가 더 생기기 때문이다.
- 0,1 범위에 있는 Sigmoid Function이 좋다.

- 이렇게 classification 분류에는 Linear regression 보다 Logistic regression이 좀더 정확하다.
Logistic functions
- Sigmoid
- Bounded
- Differentiable
- Real function
- Defined for all inputs
- Positive Derivative
- Logistic function
- Sigmoid의 특성을 가지고 있고
- Derivative를 구하기가 쉽다
- Logit function
- Logistic function의 역함수
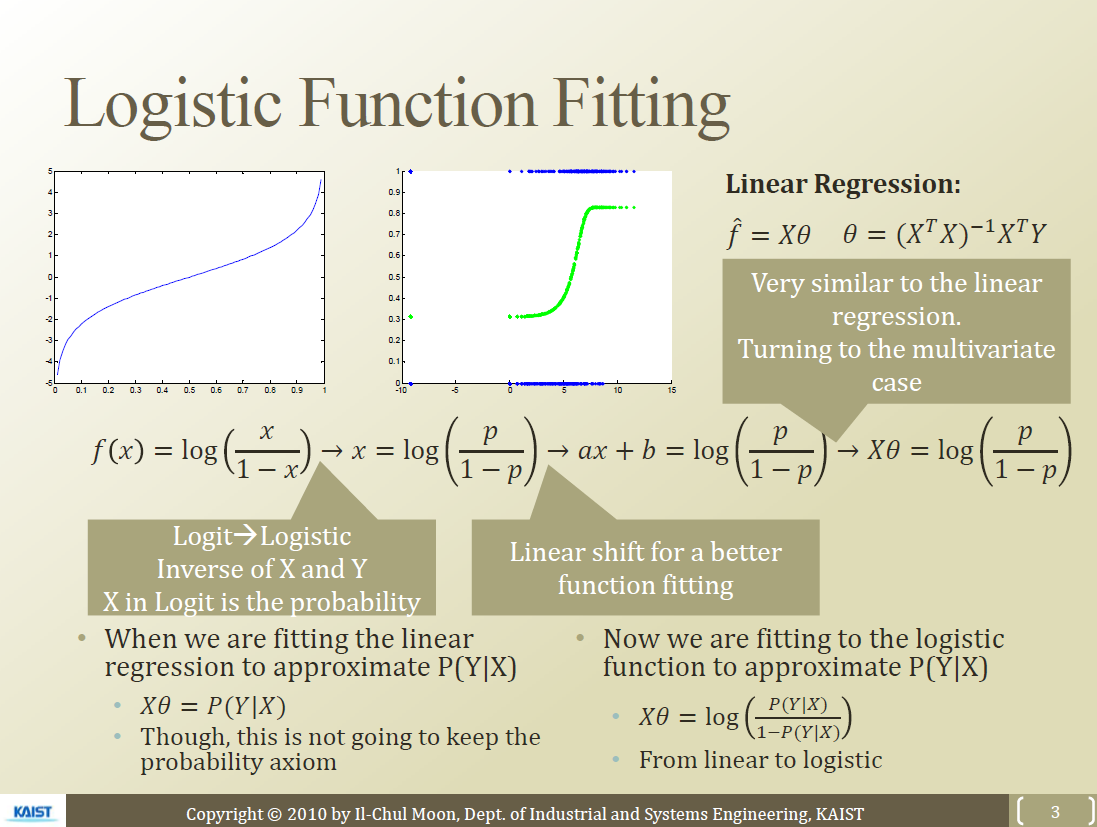
- x(A15)를 p로 모델링하면 $x=log(\frac{p}{1-p})$
- x자리에 ax+b로 넣어줌으로써 커브의 선형변환 진행
- ax+b를 벡터로 표시하면 $X\theta$
- 이걸 Logistic Function Fitting이라고 부름 (로지스틱 함수를 통해 피팅했다고 함)
Logistic regression의 적용

- Logistic function의 역함수
- 변수 $\mu$를 logistic function으로 모델링함
- 즉 반대로 logit function을 logistic function으로 고쳐주면
- 이제 중요한 것은 parameter인 $\theta$값을 추정하는 것
Finding the Parameter $\theta$
- 앞서서 배운 MLE활용
- Maximum Conditional Likelihood Estimation(MCLE) 사용

- 결과를 보면 정확한 $\theta$값이 나오지 않음
- Approximation으로 문제를 풀어야 함
- 위의 해결책으로 Gradient Descent Algorithm 사용
Gradient Method
- 테일러 시리즈(Tayler Expansion) 이용
- Point를 계속 이동해서 Update하는 것 (한 step당 이동할 방향*와 **이동 거리가 필요)

- 1) Big-Oh Notation은 해당 뒤의 오차도 Notation 안의 함수 값의 Constant를 곱한 값의 안의 범위로 포함될 할 수 있다는 것
- Order of Constant 공부!
- 2) 항상 저렇게 Big-Oh Notation값을 버릴 수 있는게 아니고 이동 거리가 매우 짧으므로 가능
- 따라서 h를 맘대로 늘리기는 좀 그럼. 적절한 h값을 잘 정해줘야 함
- 3) $hf’(x_1)u$가 최소화되기 위해서 u는 $f’(x_1)$와 반대방향이 되어야 하므로 방향이 다음과 같이 설정됨
- 4) 우리의 문제에서는 확률값을 높여야 되므로 Gradient Ascent 문제
- 즉 우리는 initial $\theta$ $\theta_0$을 설정하고 실행할 수 있음
Finding $\theta$ with Gradient Descent
- Logistic regression 문제에서 Gradient descent 알고리즘을 통해서 $\theta$ 추정치를 얻는 과정은 다음과 같다.

Linear Regression Revised
- Linear regression은 완벽히 파라미터들로 포함되는 해를 가짐
- 그러나 데이터의 개수가 많아지면 해를 구하기가 쉽지 않음
- 따라서 $\hat{\theta}=argmin_\theta (f-\hat{f})^2$ 으로 step별로 구할 수 있음
Logistic Regression과 Naive Bayes간의 관계(Gaussian Naive Naives model)
- Naive Bayes 은 Categorical input
- Logistic Regression은 Numerical input
- Continuous variable을 받을 수 있도록 Naive Bayes알고리즘 수정이 필요
-
$P(X_i=x Y=y)$을 Numerical하게 변경하는 것 - 다른 Probability model을 사용하면 됨
- ex 가우시안 분포를 잡으면 $P(X|Y,\mu,sigma^2)=\frac{1}{\sigma \sqrt{2\pi}e^{=\frac{(X)i-\mu)^2}{2\sigma^2}} }
- $P(Y=y)=\pi_1$이고 MLE등으로 값을 정할 수 있음

- 다른 Probability model을 사용하면 됨
- Naive Bayes에서 logistic regession으로 유도가 가능
- 그래서 Generative Discrimitive Pair 라고 부름




-
형태가 Logistic Regression $P(Y X)=\frac{1}{1+e^{X\theta}}$ - Gaussian Naive Bayes 은 Class로 Sorting한 경우에(+equal variance) Logistic Regerssion과 동일하다
- 그래서 Generative Discrimitive Pair 라고 부름
정리
- Naive Bayes Classifier
- Assumption
- Naive Assumption + same variance assumption
-
Gaussian Distribution for P(X Y) - Bernouli Distribution for P(Y)
- # of parameters : 2(mean)2(variance)d+1(prior)=4d+1
- Assumption
- Logistic Regression
- Assumption
- Fitting to the logistic function
- # of parameters to estimate = d+1
- Assumption
- Naive Bayes은 prior정보를 더 추가할 수 있기 때문에 Logistic Regression 보다 항상 성능이 안좋다고 볼 수는 없다
Generative-Discrimative pair
1) Discrimative Model
- $P(Y=y|X)$을 가정하는 것
- Modeling conditional probability
- Logistic Regression 2) **Generative Model** - $P(Y=y|X)=\frac{P(X|Y=y)P(Y=y)}{P(X)}$을 통해서 구하는 경우 - $P(X)$값은 normalizing constant. 직접구하진 않음. 보통 비례식으로 해서 계산함 - Baysian, Prior, Modeling Joint probability - Naive Bayes Classifier
Pros and Cons[Ng & Jordan 2002]
- Logistic regression is less biased
- Probably approximately correct learning : Naive Bayes learns faster

Leave a comment