기계학습_lec3_AAILab

참고- 문일철 교수님 유튜브-AAiKaist \ (https://www.youtube.com/watch?v=sDG1Y1vxOjs&list=PLbhbGI_ppZISMV4tAWHlytBqNq1-lb8bz&index=2)

(새롭게 알게된 정보들만 자세히 기술, 나머지 내용들은 간략하게 정리함)

Naive Bayes Classifier

• 성능도 좋고, 입문하기에 좋은 통계 모델

Optimal Classification

• Bayes Classifier
  • Error을 제일 줄이는 Optimal Classifier $f'=argmin_f P(f(X)\neq Y)$
  • 두 종류를 clasifier하는 것일시에는 $f'=argmax_{Y=y} P(Y=y|X=x)$
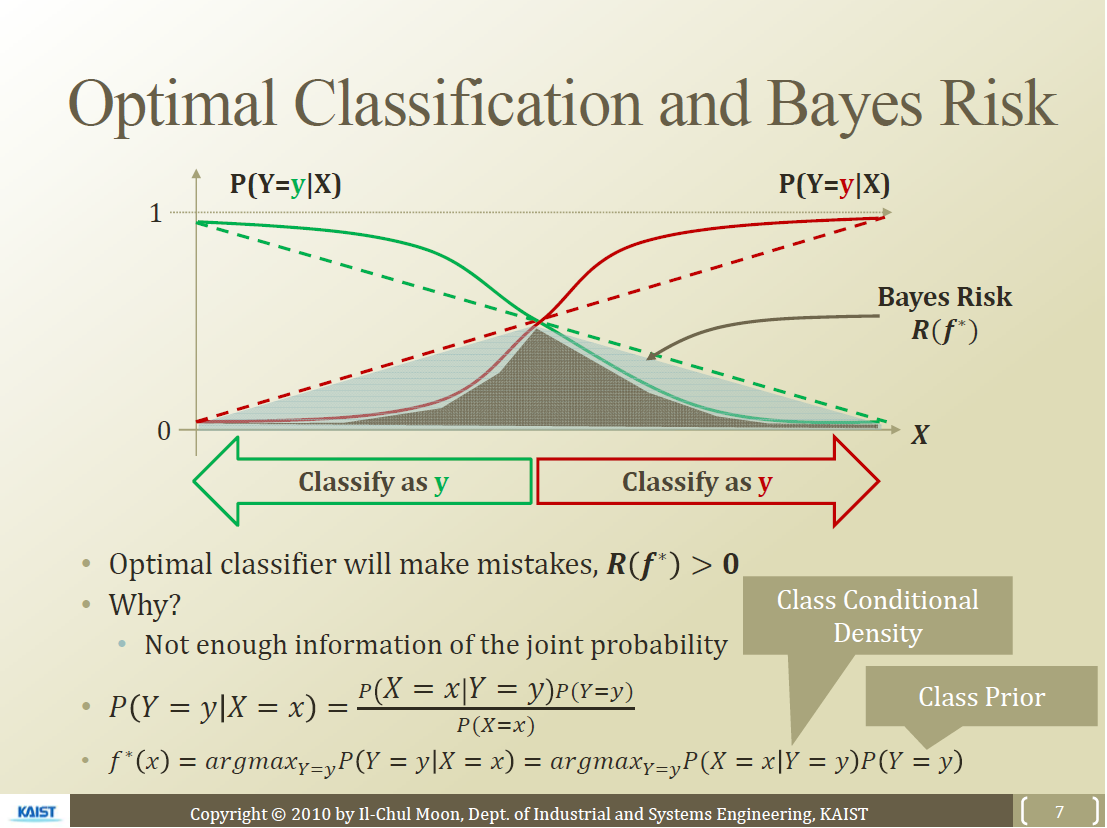
• 분류에서는 실선이 점선보다 더 좋음
  • 선형으로 되어 있으면 확률차이가 별로 크지 않음
  • error는 잘못 판별된 부위 면적에 해당됨
  • 실선 부분의 error가 더 작음
  • Decision Boundary(중점)에 대해서 높은 확률 차이로 두 class를 분류해줌
  • 위와 같은 실선 부분의 error를 줄이기 위해서 많은 방법들이 있음(ex. logistic function)
• Optimal Classifier은 다음과 같이도 표현 가능 $f'=argmax_{Y=y} P(Y=y|X=x)$ $f'=argmax_{Y=y} P(X=x|Y=y)P(Y=y)$
  • Prior : 경험 정보, 데이터에서도 취득 가능
  • Likelihood=Class Conditional Density : True인 값(Y=y)들의 확률을 계산해서 Conditional Density를 만들 수 있음
• 여러 variable 간의 Interection을 모두 존재하며 이에 따라 변수값이 엄청 많아짐
• 이러한 Interaction을 무시하는 것이 Naive Bayes filter

Naive Bayes Classifier

• 아래 조건을 풀기 위해서는 너무 파라미터의 수가 많음($(2^d-1)k$) $f'=argmax_{Y=y} P(Y=y|X=x)$
• 추가적인 조건을 걸어줘야 함

Conditional Independence

• 아래와 같이 조건부 확률을 다음과 같이 해당 조건에서 독립으로 정의하는 것 $P(X = <x_1, \cdots , x_t >|Y=y) = \Pi_i P(X_i=x_i|Y=y)$
• 따라서 y조건에서 x변수 사이에는 다음과 같은 관계가 성립함 $P(x_1,x_2|y)=P(x_1|y)P(x_2|y)$

Marginal Independence vs Conditional Independence

• 자기가 소리르 들으면 앞으로 가나 못들으면 옆의 사람 눈치를 보고 앞으로 가는 사람(예시)
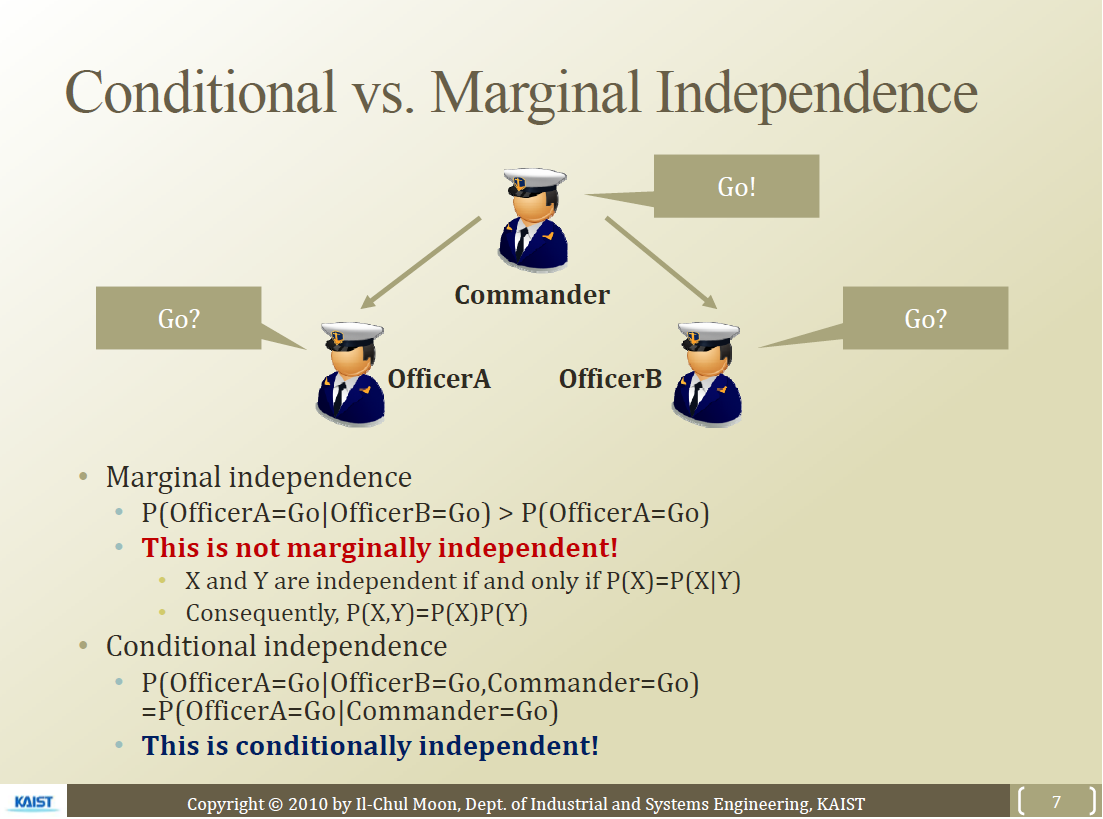
• Y가 관측이 되어 있으면 X1, X2에는 서로의 영향을 주지 않는다
• Y정보가 없으면 X1, X2는 서로 영향을 준다. $P(X)=P(X|Y)$ $P(X=x1|Y=y)=P(x=x1|y=y,X=x2)$
• 즉 Marginally independent 하지 않더라도 Conditionally independent할 수 있다.

Conditional Independence를 적용할 때

$f'=argmax_{Y=y} P(X=x|Y=y)P(Y=y)$ $\approx argmax_{Y=y}P(Y=y)\Pi_{1\leq i \leq d} P(X_i=x_i|Y=y)$

• 이게 실제로는 맞지 않음
• 너무 많은 파라미터 러닝을 없애기 위해서 만든 것일 뿐
• Assumption이 순진하군~
• 이를 Naive Bayes Classifier라고 부름

Naive Bayes Classifier

• Naive Bayes Classifier Function $f_{NH}(x) = argmax_{Y=y} P(Y=y)\Pi_{1\leq i \leq d} P(X_i=x_i|Y=y)$
• 만들기가 쉬움
• 쉬운만큼 문제점도 존재함
  • Naive Assumption의 문제
  • Incorrect Probability Estimation시 성능이 안좋음(모든 Classifier의 문제이기도 함)
    • MLE나 MAP에 대해서 진행해야 됨
• 주의 : 컴퓨터 계산시 변수가 많으면, 곱하면서 확률 값이 0에 가까워져서 0으로 인식할 수 있음, log 로 계산 진행하는 것이 더 좋음

• P(X	Y)를 유지하면서 classification을 진행하는 모델이 있는데(Logistic Regression)이를 다음 시간에 다룰 것